SOLVING PROBLEMS WITH VECTORS
Problem 1 :
Show that the vectors a = 2i + 3j + 6k, b = 6i + 2j − 3k, and c = 3i − 6j + 2k are mutually orthogonal.
Solution :
Mutually orthogonal means, they are perpendicular to each other.
a vector ⋅ b vector = (2i + 3j + 6k) ⋅ (6i + 2j − 3k)
= 2(6) + 3(2) + 6(-3)
= 12 + 6 - 18
= 18 - 18
= 0
b vector ⋅ c vector = (6i + 2j − 3k) ⋅ (3i − 6j + 2k)
= 6(3) + 2(-6) + (-3)2
= 18 - 12 - 6
= 18 - 18
= 0
c vector ⋅ a vector = (3i − 6j + 2k) ⋅ (2i + 3j + 6k)
= 3(2) + (-6)(3) + 2(6)
= 6 - 18 + 12
= 18 - 18
= 0
Since, a ⋅ b = b ⋅ c = c ⋅ a = 0, the given vectors are mutually orthogonal.
Problem 2 :
Let -i - 2j - 6k, 2i - j + k, and -i + 3j + 5k be the sides of a triangle. Show that the above vectors form a right triangle.
Solution :
The given vectors are the sides of a right triangle. To show that the triangle is a right triangle, it is enough to prove that the two of its sides are perpendicular.
Let
a = -i - 2j - 6k
b = 2i - j + k
c = = -i + 3j + 5k
a ⋅ b = (-i - 2j - 6k) ⋅ (2i - j + k)
= -1(2) + (-2)(-1) + (-6)(1)
= -2 + 2 - 6
= -6 ≠ 0
b ⋅ c = (2i - j + k) ⋅ (-i + 3j + 5k)
= 2(-1) + (-1)(3) + 1(5)
= -2 - 3 + 5
= 0
Since b ⋅ c = 0, b vector and c vector are perpendicular.
So, the given vectors form a right triangle.
Problem 3 :
If |a vector| = 5, |b vector| = 6, |c vector| = 7 and a vector + b vector + c vector = 0 vector, find a ⋅ b + b ⋅ c + c ⋅ a .
Solution :
a vector + b vector + c vector = 0 vector
|a vector + b vector + c vector| = 0
Take square on both sides.
|a vector + b vector + c vector|2 = 02
|a|2 + |b|2 + |c|2 + 2(a ⋅ b) + 2(b ⋅ c) + 2(c ⋅ a) = 0
|a|2 + |b|2 + |c|2 + 2(a ⋅ b + b ⋅ c + c ⋅ a) = 0
Substitute the given values.
52 + 62 + 72 + 2(a ⋅ b + b ⋅ c + c ⋅ a) = 0
25 + 36 + 49 + 2(a ⋅ b + b ⋅ c + c ⋅ a) = 0
110 + 2(a ⋅ b + b ⋅ c + c ⋅ a) = 0
Subtract 110 from each side.
2(a ⋅ b + b ⋅ c + c ⋅ a) = -110
Divide each side by 2.
a ⋅ b + b ⋅ c + c ⋅ a = -55
Problem 4 :
Show that the points (2, - 1, 3), (4, 3, 1) and (3, 1, 2) are coplanar.
Solution :
Let
a = 2i - j + 3k
b = 4i + 3j + k
c = 3i + j + 2k
If, three vectors are collinear, then their scalar product is zero.
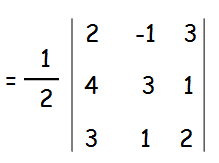
= (1/2)[2(6 - 1) + 1(8 - 3) + 3(4 - 9)]
= (1/2)[ 2(5) + 1(5) + 3(-5)]
= (1/2) [10 + 5 - 15]
= (1/2)[15 - 15]
= 0
Since the scalar product of the three vectors a, b and c zero, the given points are coplanar.
Problem 5 :
If a vector, b vector are unit vectors and θ is the angle between them, show that
(i) sin(θ/2) = (1/2)|a vector - b vector|
Solution :
In the first step, let us take square for |a vector - b vector|.
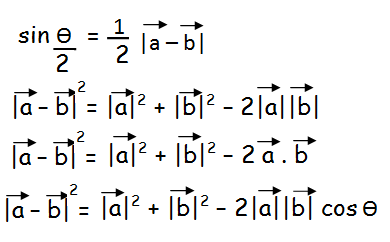
Since a vector and b vector are unit vectors, we have to apply 1 instead of a vector and b vector.
|a vector - b vector|2 = 12 + 12 - 2(1)(1)cosθ
|a vector - b vector|2 = 2 - 2cosθ
|a vector - b vector|2 = 2(1- cosθ)
|a vector - b vector|2 = 2 (2sin2 (θ/2))
|a vector - b vector| = 2sin(θ/2)
sin(θ/2) = (1/2)|a vector - b vector| ----(1)
Hence it is proved
(ii) cos(θ/2) = (1/2) |a vector + b vector|
Solution :
In the first step, let us take square for |a vector + b vector|
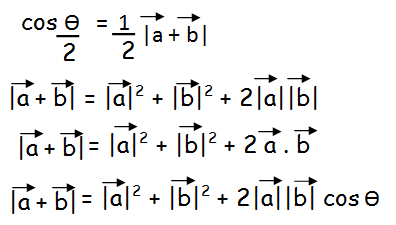
Since a vector and b vector are unit vectors, we have to apply 1 instead of a vector and b vector.
|a vector + b vector|2 = 12 + 12 + 2(1)(1)cosθ
|a vector - b vector|2 = 2 + 2cosθ
|a vector - b vector|2 = 2(1 + cosθ)
|a vector - b vector|2 = 2(2 cos2(θ/2))
|a vector - b vector| = 2cos(θ/2)
cos(θ/2) = (1/2)|a vector + b vector| ----(2)
Hence it is proved
(ii) tan(θ/2) = |a vector-b vector| / |a vector-b vector|
Solution :
We may prove the above result using (1) and (2).
sin(θ/2) = (1/2)|a vector - b vector|
cos(θ/2) = (1/2)|a vector + b vector|
(1)/(2) :
sin(θ/2)/cos(θ/2)
= (1/2)|a vector - b vector|/(1/2)|a vector + b vector|
tan(θ/2)
= (1/2)|a vector - b vector|/(1/2)|a vector + b vector|
Problem 6 :
Let a vector, b vector, c vector be three vectors such that |a vector| = 3, |b vector|= 4, |c vector|= 5, If all the three vectors are perpendicular to each other, find the value of | a vector + b vector + c vector|.
Solution :
|a + b + c|2 = |a|2 + |b|2 + |c|2 + 2(a ⋅ b + b ⋅ c + c ⋅ a)
Substitute the given values.
= 32 + 42 + 52 + 2(a ⋅ b + b ⋅ c + c ⋅ a)
Since the three a, b and c are perpendicular to each other, a ⋅ b = b ⋅ c = c ⋅ a = 0.
= 9 + 16 + 25 + 2(0 + 0 + 0)
|a + b + c|2 = 50
|a + b + c| = √50
|a + b + c| = 5√2
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 251)
Aug 08, 25 09:19 PM
Digital SAT Math Problems and Solutions (Part - 251) -
Digital SAT Math Problems and Solutions (Part - 250)
Aug 08, 25 08:05 AM
Digital SAT Math Problems and Solutions (Part - 250) -
Digital SAT Math Problems and Solutions (Part - 249)
Aug 07, 25 09:37 AM
Digital SAT Math Problems and Solutions (Part - 249)