HOW TO IDENTIFY THE TYPE OF FUNCTION IN SET THEORY

In this section, we will discuss the following types of functions with suitable examples. 

(i) one – one (injection)

(ii) many – one 

(iii) onto (Surjection)

(iv) one to one and onto  (bijection)

(iv) into

(v)  Constant function

(vi)  Identity function

(vii)  Real - valued function

One to One Function

A function f : A -> B is called one – one function if distinct elements of A have distinct images in B.

A one-one function is also called an injection.

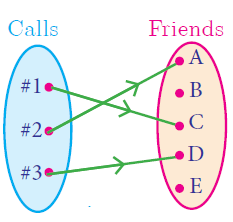
Many to One Function

A function f : A -> B is called many-one function if two or more elements of A have same image in B.

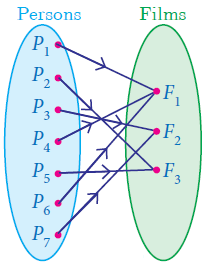
In other words, a function f : A-> B is called many-one if f it is not one–one.

Onto Function

A function f : A -> B is said to be onto function if the range of f is equal to the co-domain of f.

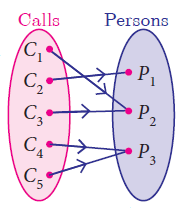
In other words, every element in the co-domain B has a pre-image in the domain A. An onto function is also called a surjection.

One to One and Onto Function

A function f : A -> B is called an into function if there exists atleast one element in B which is not the image of any element of A.

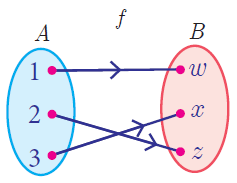
In other words, every element in the co-domain B has a pre-image in the domain A. An onto function is also called a surjection.

Into Function

Distinct elements of A have distinct images in B and every element in B has a pre-image in A.

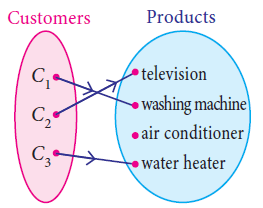
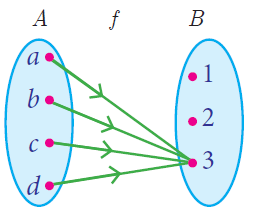
Constant Function

A function f : A -> B is called a constant function if the range of f contains only one element. That is, f (x ) = c , for all x ∊ A and for some fixed c ∊ B .

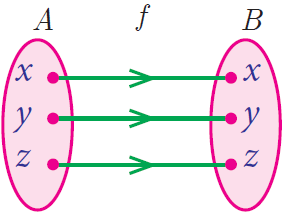
Identity Function

Let A be a non–empty set. Then the function f : A -> A defined by f (x) = x for all x ∊ A is called an identity function on A and is denoted by I_A.

Problem 1 :

Is a constant function a linear function?

Solution :

Let us consider an example of constant function,

f(x) = 3

f(x) = y

y = 3

The graphical form of the above function is a staright line (horizontal). Then it can be considered as linear function. Then yes, a constant function is a linear function.

Problem 2 :

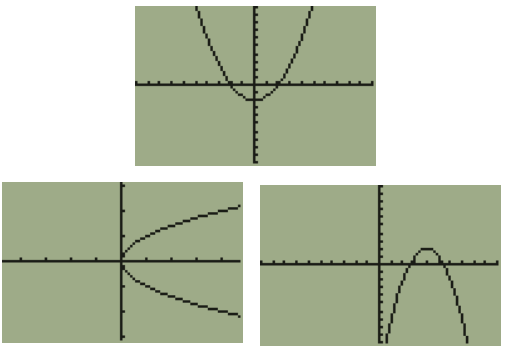
Is quadratic function a one – one function?

Solution :

The function can be said as one to one when each input has different and unique outputs.

When graph of function is given by drawing the horizontal line, when the horizontal line intersects the graph at most one point we will decide it is one to one. But graph of quadratic function will not pass the horizontal line test. Then quadratic function is not a one to one function.

Problem 3 :

Is cubic function a one – one function?

Solution :

Yes, a cubic function is generally considered a one-to-one function

Problem 4 :

Is the reciprocal function a bijection?

Solution :

A function can be said as bijective when codomain and range are the same for the function. Then reciprocal function is bijective.

Problem 5 :

If f A: --> B is a constant function, then the range of f will have ____ elements.

Solution :

A function which has the same value as output for every different inputs, then it is called constant function. 

Thne, 

If f A: --> B is a constant function, then the range of f will have one element.

Problem 6 :

If n(A x B) = 6 and A = {1, 3} then n(B) is 

a) 1   b)  2    c)  3     d)  6

Solution :

n(A x B) = 6 and A = {1, 3} then n(B)

In general, n(AxB) = n(A) x n(B)

n(A) = 2

n(AxB) = n(A) x n(B)

6 = 2 x n(B)

n(B)  = 6/2

n(B) = 3

Problem 7 :

If A = {a, b, q}, B = {2, 3}, C = {p, q, r, s} then n [(A u C) x B] is 

a)  8   b)  20    c)   12    d) 16

Solution :

A = {a, b, q}, B = {2, 3}, C = {p, q, r, s}

n [(A u C) x B]  :

A U B = {a, b, q, p, r, s}

n(A U C) = 6

n [(A u C) x B]  = n(A u C) x n(B)

n(B) = 2

Applying these values, we get

= 6 x 2

= 12

Problem 8 :

If the ordered pairs (a + 2, 4) and (5, 2a + b) are equal then a + b is 

a)  (2, -2)   b)  (5, 1)    c)  (2, 3)    d) (3, -2)

Solution :

(a + 2, 4) = (5, 2a + b)

By equating the corresponding terms, we get

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.