HOW TO IDENTIFY FUNCTION FROM GRAPH

Example 1 : 

Use the vertical line test to determine whether the following graph represents a function.

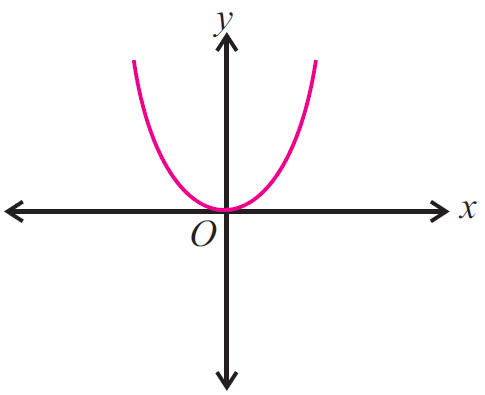
Solution :

Step 1 :

Draw a vertical line at any where on the given graph.

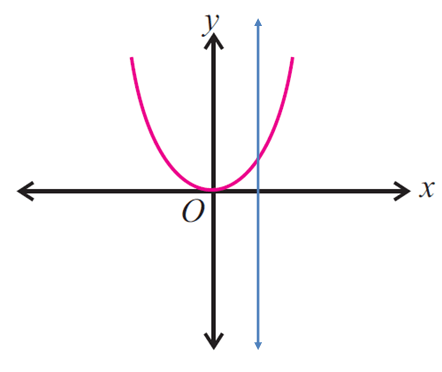
Step 2 :

We have to check whether the vertical line drawn on the graph intersects the graph in at most one point.

Step 3 :

In the above graph, the vertical line intersects the graph in at most one point, then the given graph represents a function.

Example 2 :

Use the vertical line test to determine whether the following graph represents a function.

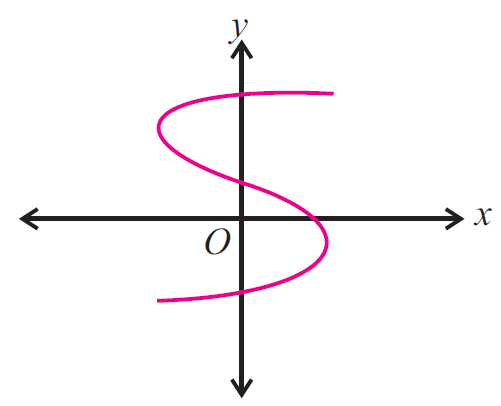
Solution :

Step 1 :

Draw a vertical line at any where on the given graph.

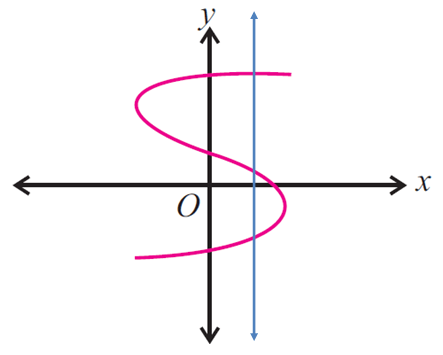
Step 2 :

We have to check whether the vertical line drawn on the graph intersects the graph in at most one point.

Step 3 :

In the above graph, the vertical line intersects the graph in more than one point (three points), then the given graph does not represent a function.

Example 3 :

Use the vertical line test to determine whether the following graph represents a function.

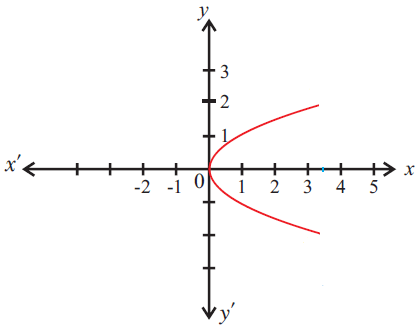
Solution :

Step 1 :

Draw a vertical line at any where on the given graph.

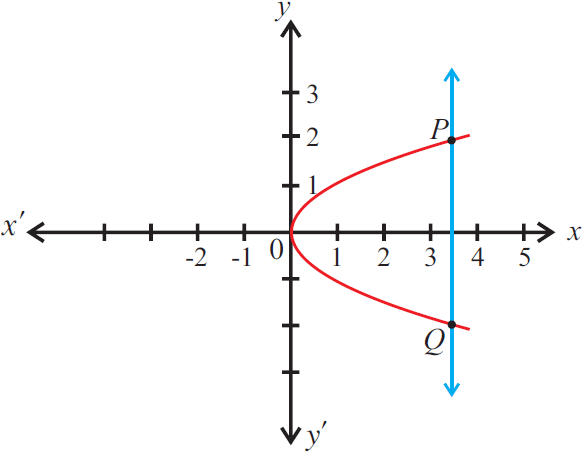
Step 2 :

We have to check whether the vertical line drawn on the graph intersects the graph in at most one point.

Step 3 :

In the above graph, the vertical line intersects the graph in more than one point (three points), then the given graph does not represent a function.

Example 4 :

Use the vertical line test to determine whether the following graph represents a function.

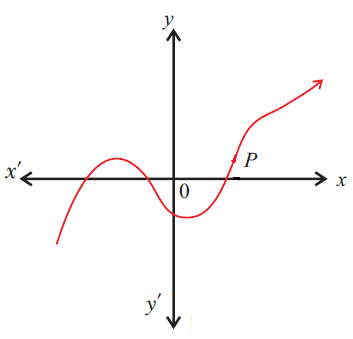
Solution :

Step 1 :

Draw a vertical line at any where on the given graph.

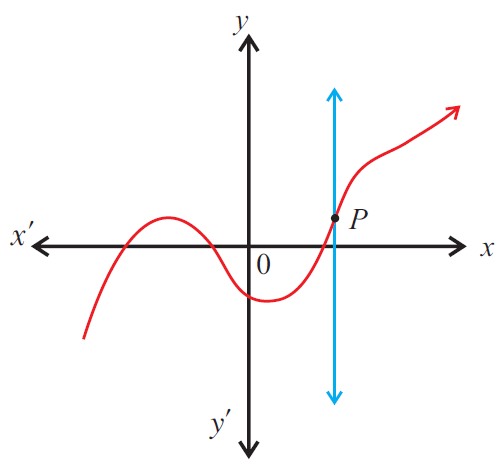
Step 2 :

We have to check whether the vertical line drawn on the graph intersects the graph in at most one point.

Step 3 :

In the above graph, the vertical line intersects the graph in at most one point, then the given graph represents a function.

Example 5 :

Use the vertical line test to determine whether the following graph represents a function.

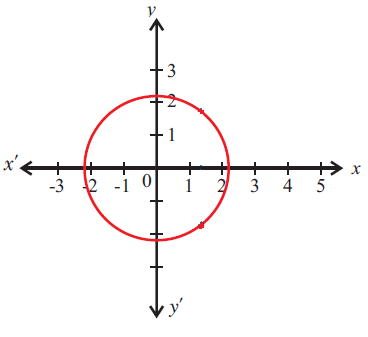
Solution :

Step 1 :

Draw a vertical line at any where on the given graph.

Step 2 :

We have to check whether the vertical line drawn on the graph intersects the graph in at most one point.

Step 3 :

In the above graph, the vertical line intersects the graph in more than one point (three points), then the given graph does not represent a function.

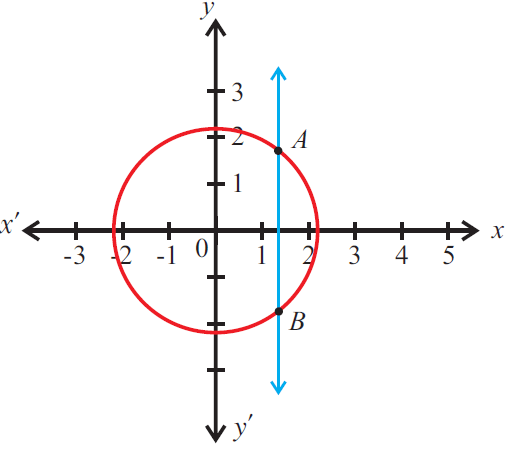
Example 6 :

Is the relationship a function? Justify your answer. Use the words “input” and “output” in your explanation, and connect them to the context represented by the graph.

Rachel plans to study 2 hours for her next exam. How might plotting her grade on the same graph change your answer to above question ?

Solution :

Yes, the above relationship is a function. When we draw a vertical line, it is intersecting the graph maximum once.

When the number of hours is 2, then the grade will be 95.

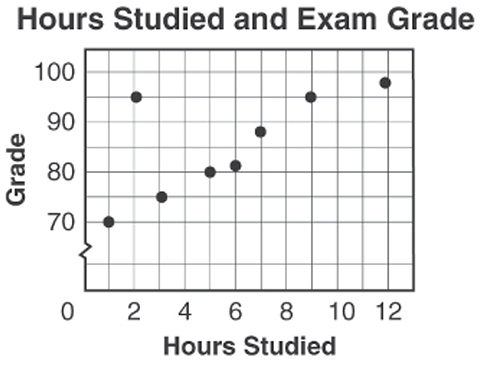
Example 7 :

The graph shows the relationship between the number of hours students spent studying for an exam and the exam grades. Is the relationship represented by the graph a function?

Solution :

The input values are the number of hours spent studying by each student. The output values are the exam grades. The points represent the following ordered pairs:

(1, 70) (2, 70) (2, 85) (3, 75) (5, 80) (6, 82) (7, 88) (9, 90) (9, 95) (12, 98)

Notice that 2 is paired with both 70 and 85, and 9 is paired with both 90 and 95. Therefore, since these input values are paired with more than one output value, the relationship is not a function.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.