HOW TO GRAPH CIRCLES

Graph the circles whose equations are given :

Example 1 :

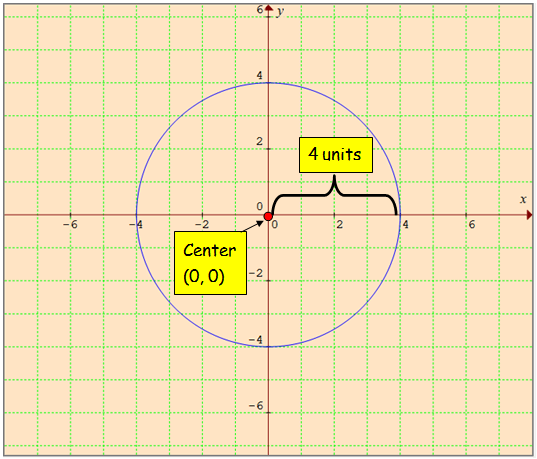
x² + y² = 16

Solution :

The the given equation is in the form of

x² + y² = r².

Center of the circle is (0, 0). 

r² = 16

r = √16

radius = 4 units

Example 2 :

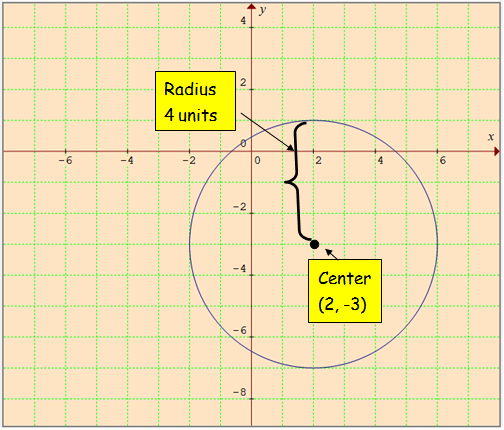
(x - 2)² + (y + 3)² = 16

Solution :

The the given equation of the circle is in the form of

(x - h)² + (y - k)² = r² ----(1)

Center of the circle is (h, k) and radius is r.

(x - 2)² + (y + 3)² = 16

(x - 2)² + (y - (-3))² = 4² ----(2)

Comparing (1) and (2),

center (h, k) = (2, -3)

r² = 4²

r = 4

radius = 4 units

Example 3 :

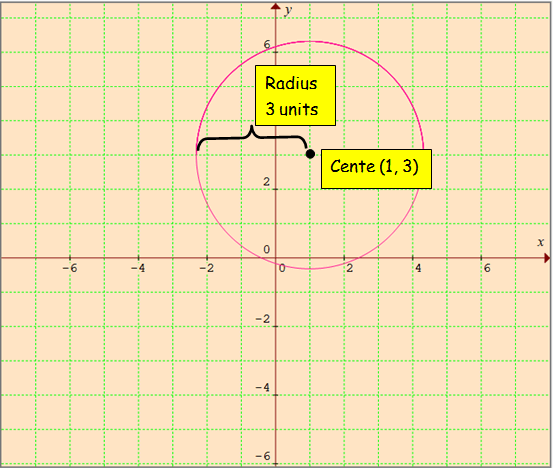
x² + y² - 2x - 6y + 1 = 0

Solution :

The equation of the  given circle is in general form

x² + y²+ 2gx + 2fy + c = 0 ----(1)

center = (-g, -f)

radius = √(g² + f² - c)

x² + y² - 2x - 6y + 1 = 0 ----(2)

Comparing (1) and (2),

2g = -2 ----> g = -1 ----> -g = 1

2f = -6 ----> f = -3 ----> -f = 3

center (-g, -f) = (1, 3)

radius = √(g² + f² - c)

= √(1² + 3² - 1)

= √(1 + 9 - 1)

= √9

r = 3 units

Example 4 :

Give the equation of the circle whose center is (4, - 3) and goes through (1, 5).

Solution :

Center is (4, -3) and passes through the point (1, 5)

Distance between the points (4, -3) and (1, 5).

Radius = distance between center and one of the points of the circle.

= √(x₂ - x₁)² + (y₂ - y₁)²

= √(4 - 1)² + (-3 - 5)²

= √3² + (-8)²

= √(9 + 64)

= √73

Equation of circle :

(x - h)² + (y - k)² = r²

(x - 4)² + (y - (-3))² = √73²

(x - 4)² + (y + 3)² = 73

x² - 8x + 16 + y² + 6y + 9 = 73

x² + y² - 8x + 6y + 16 + 9 - 73 = 0

x² + y² - 8x + 6y - 48 = 0

Question 5 :

Give the equation of circle whose endpoints of a diameter at (4, -1) and (4, -5)

Solution :

Endpoint of the diameter (4, -1) and (4, -5)

= (x₁ + x₂)/2, (y₁ + y₂)/2

= (4 + 4)/2, (-1 - 5)/2

= 8/2, -6/2

= (4, -3)

Center of the circle is (4, -3).

Radius = distance between center and one of the points of the circle.

= √(x₂ - x₁)² + (y₂ - y₁)²

= √(4 - 4)² + (-3 - (-1))²

= √0² + (-3 + 1)²

= √(-2)²

= √4

= 2

Equation of circle :

(x - h)² + (y - k)² = r²

(x - 4)² + (y - (-3))² = 2²

(x - 4)² + (y + 3)² = 2²

x² - 2x(4) + 4² + y² + 2y(3) + 3² = 4

x² - 8x + y² + 6y + 16 + 9 = 4

x² + y² - 8x + 6y + 25 - 4 = 0

x² + y² - 8x + 6y + 21 = 0

Question 6 :

Graph the circles 

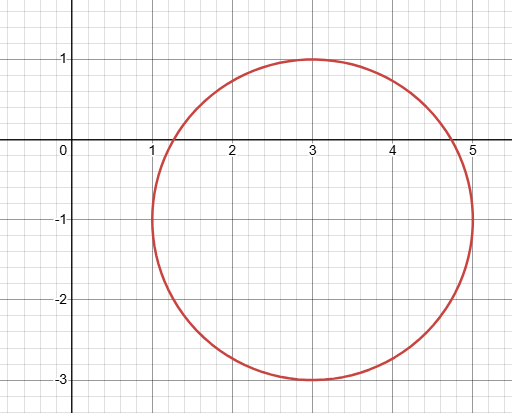
a) (x - 3)² + (y + 1)² = 4

b)  (x - 2)² + (y - 5)² = 9

c)  (y + 4)² + (x + 2)² = 4

Solution :

a) (x - 3)² + (y + 1)² = 4

(x - 3)² + (y - (-1))² = 2²

Comparing with (x - h)² + (y - k)² = r²

Here center (h, k) is (-3, -1) and radius = 2

b)  (x - 2)² + (y - 5)² = 9

(x - 2)² + (y - 5)² = 3²

Comparing with (x - h)² + (y - k)² = r²

Here center (h, k) is (2, 5) and radius = 3

c)  (y + 4)² + (x + 2)² = 4

(y + 4)² + (x + 2)² = 4

 (x + 2)² + (y + 4)² = 4

 (x - (-2))² + (y - (-4))² = 2²

Comparing with (x - h)² + (y - k)² = r²

Here center (h, k) is (-2, -4) and radius = 2

Question 7 :

A circle has equation x² + y² = 100.

(a) Write down the co-ordinates of the centre of the circle.

(b) Write down the radius of the circle.

Solution :

x² + y² = 100

x² + y² = 10²

Center of the circle is (0, 0) and radius of the circle is 10.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.