HOW TO GRAPH A PARABOLA IN VERTEX FORM

Example 1 : 

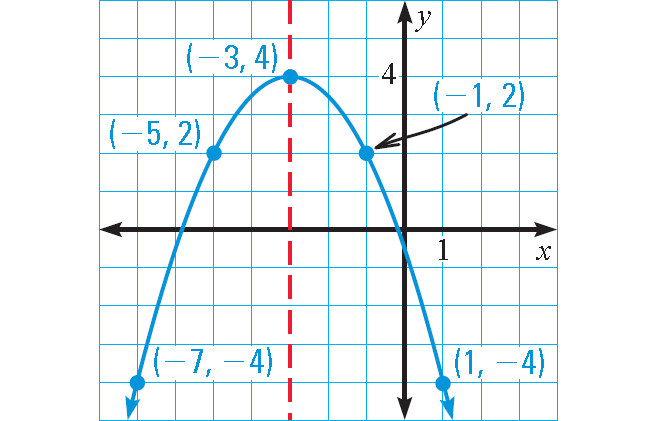
Graph : y = -½(x + 3)² + 4

Solution : 

Equation of the parabola is in vertex form : 

y = a(x - h)² + k

a = -½, h = -3, and k = 4

Because a < 0, the parabola opens down.

To graph the function, first plot the vertex (h, k) = (-3, 4).

Draw the axis of symmetry x = -3. 

Plot two points on one side of it, such as (-1, 2) and (1, -4). Use symmetry to plot two more points, such as (-5, 2) and (-7, -4). 

Use symmetry to complete the graph.

Example 2 : 

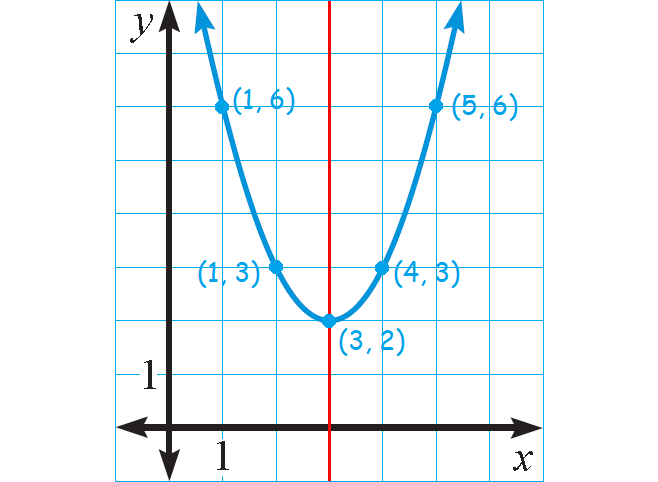
Graph :  y = (x - 3)² + 2

Solution : 

Equation of the parabola is in vertex form : 

y = a(x - h)² + k

a = 1, h = 3, and k = 2

Because a < 0, the parabola opens down.

To graph the function, first plot the vertex (h, k) = (3, 2).

Draw the axis of symmetry x = 3

Plot two points on one side of it, such as (1, 3) and (1, 6). Use symmetry to plot two more points, such as (4, 3) and (5, 6).

Use symmetry to complete the graph.

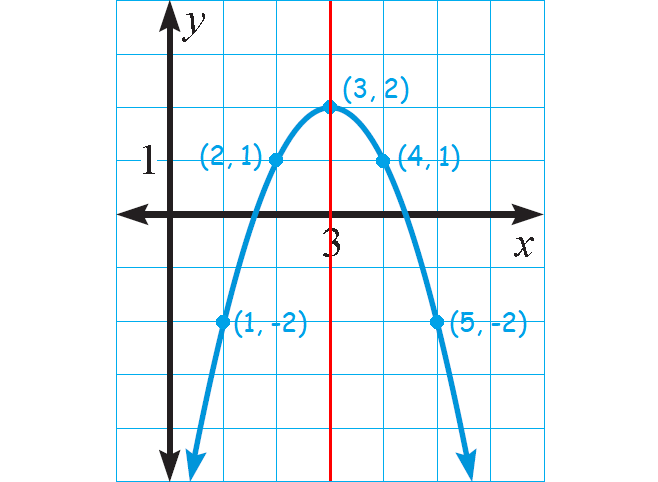
Example 3 : 

Graph : y = -(x - 3)² + 2

Solution : 

Equation of the parabola is in vertex form : 

y = a(x - h)² + k

a = -1, h = 3, and k = 2

Because a < 0, the parabola opens down.

To graph the function, first plot the vertex (h, k) = (3, 2).

Draw the axis of symmetry x = 3. 

Plot two points on one side of it, such as (2, 1) and (1, -2).  Use symmetry to plot two more points, such as (4, 1) and (5, -2).

Use symmetry to complete the graph.

Sketch the graphs of the following functions without using tables of values and state the coordinates of vertex.

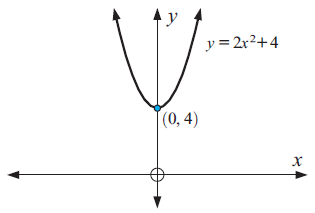
Example 4 :

Graph : y = 2x² + 4

Solution : 

Equation of the parabola is in vertex form : 

y = a(x - h)² + k

y = 2(x - 0)² + 4

a = 2, h = 0 and k = 4

Because a > 0, the parabola opens up.

To graph the function, first plot the vertex (h, k) = (0, 4).

Draw the axis of symmetry x = 4. 

Finding x-intercept :

y = 2x² + 4

Put y = 0

2x² + 4 = 0

2x² = -4

x² = -2

x = not a real value, so there is no x-intercept.

Finding y-intercept :

y = 2x² + 4

Put x = 0

y = 2(0)² + 4

y = 4

Example 5 :

Graph : y = -(x - 2)² + 4

Solution : 

Equation of the parabola is in vertex form : 

y = a(x - h)² + k

y = -(x - 2)² + 4

a = -1, h = 2 and k = 4

Because a < 0, the parabola opens down.

To graph the function, first plot the vertex (h, k) = (2, 4).

Draw the axis of symmetry x = 2. 

Finding x-intercept :

y = -(x - 2)² + 4

Put y = 0

-(x - 2)² + 4 = 0

-(x - 2)² = -4

(x - 2)² = 4

x - 2 = ±4

x-intercepts are (6, 0) and (-2, 0).

Finding y-intercept :

y = -(x - 2)² + 4

Put x = 0

y = -(0 - 2)² + 4

y = -4 + 4

y = 0

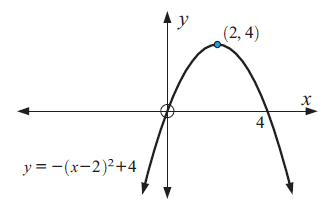
Example 6 :

Graph : y = 3(x + 1)² - 4

Solution : 

Equation of the parabola is in vertex form : 

y = a(x - h)² + k

y = 3(x + 1)² - 4

a = 3, h = -1 and k = -4

Because a > 0, the parabola opens up.

To graph the function, first plot the vertex (h, k) = (-1, -4).

Draw the axis of symmetry x = -1. 

Finding x-intercept :

y = 3(x + 1)² - 4

Put y = 0

3(x + 1)² - 4 = 0

3(x + 1)² = 4

(x + 1)² = 4/3

(x + 1) = √(4/3)

x + 1 = ±2/√3

x-intercepts are (0.15, 0) and (-2.15, 0).

Finding y-intercept :

y = 3(x + 1)² - 4

Put x = 0

y = 3(0 + 1)² - 4

y = 3 - 4

y = -1

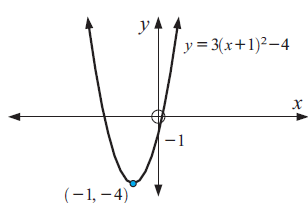
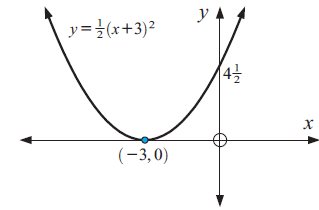
Example 7 :

Graph : y = (1/2)(x + 3)²

Solution : 

Equation of the parabola is in vertex form : 

y = a(x - h)² + k

y = (1/2)(x + 3)²

a = 1/2, h = -3 and k = 0

Because a > 0, the parabola opens up.

To graph the function, first plot the vertex (h, k) = (-3, 0).

Draw the axis of symmetry x = -3. 

Finding x-intercept :

y = (1/2)(x + 3)²

Put y = 0

(1/2)(x + 3)² = 0

(x + 3)² = 0

x + 3 = 0

x = -3

x-intercept is (-3, 0).

Finding y-intercept :

y = (1/2)(x + 3)²

Put x = 0

y = (1/2)(0 + 3)²

y = 9/2

y = 4.5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.