HOW TO FIND THE VERTEX OF A PARABOLA

Vertex of a Parabola (Opens Up/Down)

The vertex of a parabola is the point where the parabola crosses its axis of symmetry.

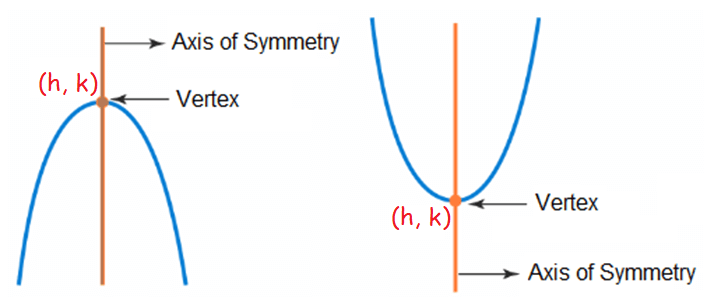
The vertex of a parabola is the highest or lowest point which is also known as maximum or minimum value.

If a parabola opens up, the vertex will be the lowest point and if it opens down, the vertex will be the highest point of the parabola.

Equation of a parabola in standard form :

y = ax² + bx + c

Equation of a parabola in vertex form :

y = a(x - h)² + k

where (h, k) is the vertex.

In both standard form and vertex form, if

a < 0 ----> parabola opens down

a > 0 ----> parabola opens up

When the equation of a parabola is given in standard form, you can find the vertex of the parabola in two methods.

Method 1 :

Let the equation of a parabola be y = ax² + bx + c.

You can use the formula given below to find the x-coordinate of the vertex.

x = ⁻ᵇ⁄₂ₐ

After having found the x-coordinate, you can substitute it into the equation of the parabola and find the y-coordinate of the vertex.

Method 2 :

You can write the given equation of a parabola in vertex form and find the vertex.

Video Lesson

In each case, find the vertex of the parabola :

Example 1 :

y = x² - 2x - 5

Solution :

Method 1 :

Comparing y = ax² + bx + c and y = x² - 2x - 5,

a = 1, b = -2 and c = -5

x-coordinate of the vertex :

x = ⁻ᵇ⁄₂ₐ

Substitute a = 1 and b = -2.

x = ⁻⁽⁻²⁾⁄₂₍₁₎

x = ²⁄₂

x = 1

y-coordinate of the vertex :

Substitute x = 1 in y = x² - 2x - 5.

y = 1² - 2(1) - 5

y = 1 - 2 - 5

y = -6

Vertex of the parabola is (1, -6)

Method 2 :

Write the given equation of parabola in vertex form.

y = x² - 2x - 5

y = x² - 2(x)(1) + 1² - 1² - 5

Using the identity (a - b)² = a² - 2ab + b²,

y = (x - 1)² - 1² - 5

y = (x - 1)² - 1 - 5

y = (x - 1)² - 6

Comparing y = a(x - h)² + k and y = (x - 1)² - 6,

h = 1 and k = -6

Vertex of the parabola :

(h, k) = (1, -6)

Example 2 :

y = -x² - 14x - 59

Solution :

Method 1 :

Comparing y = ax² + bx + c and y = -x² - 14x - 59,

a = -1, b = -14 and c = -59

x-coordinate of the vertex :

x = ⁻ᵇ⁄₂ₐ

Substitute a = -1 and b = -14.

x = ⁻⁽⁻¹⁴⁾⁄₂₍₋₁₎

x = ¹⁴⁄₋₂

x = -7

y-coordinate of the vertex :

Substitute x = -7 in y = -x² - 14x - 59.

y = -(-7)² - 14(-7) - 59

y = -49 + 98 - 59

y = -10

Vertex of the parabola is (-7, -10)

Method 2 :

Write the given equation of parabola in vertex form.

y = -x² - 14x - 59

y = -1(x² + 14x) - 59

y = -1[x² + 2(x)(7) + 7² - 7²] - 59

Using the identity (a + b)² = a² + 2ab + b²,

y = -1[(x + 7)² - 7²] - 59

y = -1[(x + 7)² - 49] - 59

y = -1(x + 7)² + 49 - 59

y = -1(x + 7)² - 10

The vertex form equation y = -1(x + 7)² - 10 can be written as

y = -1[x - (-7)]² + (-10)

Comparing the above equation and y = a(x - h)² + k,

h = -7 and k = -10

Vertex of the parabola :

(h, k) = (-7, -10)

Example 3 :

y = x² + 4x

Solution :

Method 1 :

Comparing y = ax² + bx + c and y = x² + 4x,

a = 1, b = 4 and c = 0

x-coordinate of the vertex :

x = ⁻ᵇ⁄₂ₐ

Substitute a = 1 and b = 4.

x = ⁻⁴⁄₂₍₁₎

x = ⁻⁴⁄₂

x = -2

y-coordinate of the vertex :

Substitute x = -2 in y = x² + 4x.

y = (-2)² + 4(-2)

y = 4 - 8

y = -4

Vertex of the parabola is (-2, -4)

Method 2 :

Write the given equation of parabola in vertex form.

y = x² + 4x

y = x² + 2(x)(2) + 2² - 2²

Using the identity (a + b)² = a² + 2ab + b²,

y = (x + 2)² - 2²

y = (x + 2)² - 4

The vertex form equation y = (x + 2)² - 4 can be written as

y = [x - (-2)]² + (-4)

Comparing the above equation and y = a(x - h)² + k,

h = -2 and k = -4

Vertex of the parabola :

(h, k) = (-2, -4)

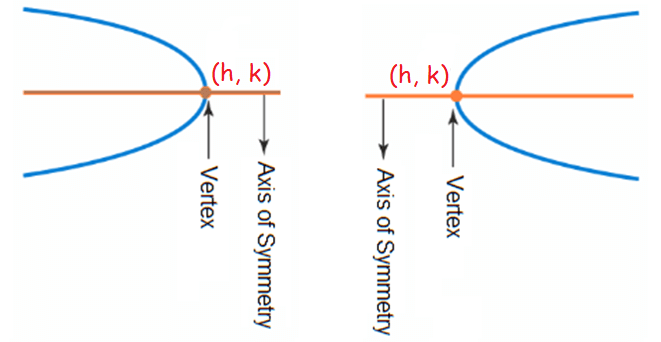
Vertex of a Parabola (Opens to the Left/Right)

Equation of a parabola in standard form :

x = ay² + by + c

Equation of a parabola in vertex form :

x = a(y - k)² + h

where (h, k) is the vertex.

In both standard form and vertex form, if

a < 0 ----> parabola opens to the left

a > 0 ----> parabola opens up to the right

When the equation of a parabola is given in standard form, you can find the vertex of the parabola in two methods.

Method 1 :

Let the equation of a parabola be x = ay² + by + c.

You can use the formula given below to find the y-coordinate of the vertex.

y = ⁻ᵇ⁄₂ₐ

After having found the y-coordinate, you can substitute it into the equation of the parabola and find the x-coordinate of the vertex.

Method 2 :

You can write the given equation of a parabola in vertex form and find the vertex.

In each case, find the vertex of the parabola :

Example 4 :

x = y² - 2y - 5

Solution :

Method 1 :

Comparing x = ay² + by + c and x = y² - 2y - 5,

a = 1, b = -2 and c = -5

y-coordinate of the vertex :

y = ⁻ᵇ⁄₂ₐ

Substitute a = 1 and b = -2.

y = ⁻⁽⁻²⁾⁄₂₍₁₎

y = ²⁄₂

y = 1

x-coordinate of the vertex :

Substitute y = 1 in x = y² - 2y - 5.

x = 1² - 2(1) - 5

x = 1 - 2 - 5

x = -6

Vertex of the parabola is (-6, 1)

Method 2 :

Write the given equation of parabola in vertex form.

x = y² - 2y - 5

x = y² - 2(y)(1) + 1² - 1² - 5

Using the identity (a - b)² = a² - 2ab + b²,

x = (y - 1)² - 1² - 5

x = (y - 1)² - 1 - 5

x = (y - 1)² - 6

Comparing x = a(y - k)² + h and y = (x - 1)² - 6,

h = -6 and k = 1

Vertex of the parabola :

(h, k) = (-6, 1)

Example 5 :

x = -y² - 14y - 59

Solution :

Method 1 :

Comparing x = ay² + by + c and x = -y² - 14y - 59,

a = -1, b = -14 and c = -59

x-coordinate of the vertex :

y = ⁻ᵇ⁄₂ₐ

Substitute a = -1 and b = -14.

y = ⁻⁽⁻¹⁴⁾⁄₂₍₋₁₎

y = ¹⁴⁄₋₂

y = -7

y-coordinate of the vertex :

Substitute y = -7 in x = -y² - 14y - 59.

x = -(-7)² - 14(-7) - 59

x = -49 + 98 - 59

x = -10

Vertex of the parabola is (-10, -7)

Method 2 :

Write the given equation of parabola in vertex form.

x = -y² - 14y - 59

x = -1(y² + 14y) - 59

x = -1[y² + 2(y)(7) + 7² - 7²] - 59

Using the identity (a + b)² = a² + 2ab + b²,

x = -1[(y + 7)² - 7²] - 59

x = -1[(y + 7)² - 49] - 59

x = -1(y + 7)² + 49 - 59

x = -1(y + 7)² - 10

The vertex form equation x = -1(y + 7)² - 10 can be written as

x = -1[y - (-7)]² + (-10)

Comparing the above equation and x = a(y - k)² + h,

h = -10 and k = -7

Vertex of the parabola :

(h, k) = (-10, -7)

Example 6 :

x = y² + 4y

Solution :

Method 1 :

Comparing x = ay² + by + c and x = y² + 4y,

a = 1, b = 4 and c = 0

x-coordinate of the vertex :

y = ⁻ᵇ⁄₂ₐ

Substitute a = 1 and b = 4.

y = ⁻⁴⁄₂₍₁₎

y = ⁻⁴⁄₂

y = -2

y-coordinate of the vertex :

Substitute y = -2 in x = y² + 4y.

x = (-2)² + 4(-2)

x = 4 - 8

x = -4

Vertex of the parabola is (-4, -2).

Method 2 :

Write the given equation of parabola in vertex form.

x = y² + 4y

x = y² + 2(y)(2) + 2² - 2²

Using the identity (a + b)² = a² + 2ab + b²,

x = (y + 2)² - 2²

x = (y + 2)² - 4

The vertex form equation x = (y + 2)² - 4 can be written as

x = [y - (-2)]² + (-4)

Comparing the above equation and x = a(y - k)² + h,

h = -4 and k = -2

Vertex of the parabola :

(h, k) = (-4, -2)

Example 7 :

y = -3(x + 2)(x - 6)

Solution :

y = -3(x + 2)(x - 6)

Substitute y = 0 to find the x-intercepts of the parabola above.

-3(x + 2)(x - 6) = 0

Divide both sides by -3.

-3(x + 2)(x - 6) = 0

x + 2 = 0  or  x - 6 = 0

x = -2  or  x = 6

x-coordinate of the vertex :

x = ⁽⁻² ⁺ ⁶⁾⁄₂

x = ⁴⁄₂

x = 2

y-coordinate of the vertex :

Substitute x = 2 in y = -3(x + 2)(x - 6).

y = -3(2 + 2)(2 - 6)

y = -3(4)(-4)

y = 48

Vertex of the parabola is (2, 48).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.