HOW TO FIND VALUES OF TRIGONOMETRIC FUNCTIONS FROM THE TERMINAL SIDE

Example 1 :

(5/7, 2√6/7) is a point on the terminal side of an angle θ in standard position. Determine the trigonometric function values of angle θ.

Solution :

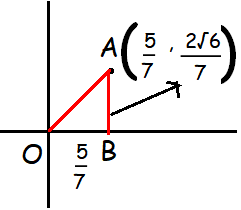
First let us mark the given point in a graph paper and draw a triangle.

OA2  =  OB2 + AB2 OA2  =  (5/7)2 + (2√6/7)2   =  25/49 + 24/49 OA  =  1

Opposite side  =  AB  =  2√6/7

Adjacent side  =  OB  =  5/7

Hypotenuse side  =  OA  =  1

Example 2 :

Find the values of other five trigonometric functions for the following:

(i) cos θ = -1/2, θ lies in the III quadrant.

(ii) cos θ = 2/3, θ lies in the I quadrant.

Solution :

(i) cos θ = -1/2, θ lies in the III quadrant.

cos θ  =  Adjacent side/hypotenuse side

cos θ  =  -1/2

Adjacent side  =  1, Hypotenuse side  =  2

(Hypotenuse side)²  =  (Opposite side)² + (Adjacent side)²

Opposite side  =  √2² - 1²

  =  √(4 - 1)

  =  √3

Opposite side  =  √3

Note : Since θ  lies in 3^rd quadrant, all trigonometric ratios other than tan  and cot will have negative sign.

sin θ  =  Opposite side/hypotenuse side  =  -√3/2

tan θ  =  Opposite side/Adjacent side  =  √3/1  =  -√3

cosec θ  =  Hypotenuse side/Opposite side  =  2/√3

sec θ  =  Hypotenuse side/Adjacent side  =  2/1  =  2

cot θ  =  Adjacent side/Opposite side  =  -1/√3

(ii) cos θ = 2/3, θ lies in the I quadrant.

Solution :

cos θ  =  Adjacent side/hypotenuse side

cos θ  =  2/3

Adjacent side  =  2, Hypotenuse side  =  3

(Hypotenuse side)²  =  (Opposite side)² + (Adjacent side)²

Opposite side  =  √3² - 2²

  =  √(9 - 4)

  =  √5

Opposite side  =  √5

Note : Since θ  lies in 1^st quadrant, all trigonometric ratios will be positive.

sin θ  =  Opposite side/hypotenuse side  =  √5/3

tan θ  =  Opposite side/Adjacent side  =   √5/2

cosec θ  =  Hypotenuse side/Opposite side  =  3/√5

sec θ  =  Hypotenuse side/Adjacent side  =  3/2

cot θ  =  Adjacent side/Opposite side  =  2/√5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.