HOW TO FIND THE TRANSPOSE OF A MATRIX

Transpose of a matrix :

The matrix which is obtained by interchanging the elements in rows and columns of the given matrix A is called transpose of A and is denoted by A^T (read as A transpose).

If order of A is m x n then order of A^T is n x m . We note that (A^T )^T = A.

Question 1 :

If A =

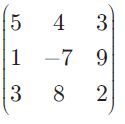
find A^T.

Solution :

To find the transpose of the given matrix, we have to write the elements in the rows as columns and the elements in the columns as rows.

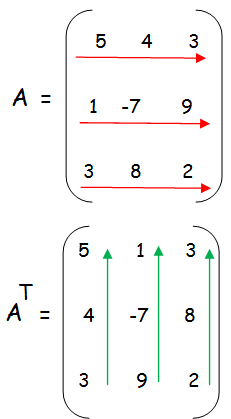
Question 2 :

If A =

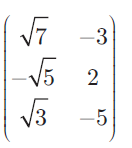
find -A^T.

Solution :

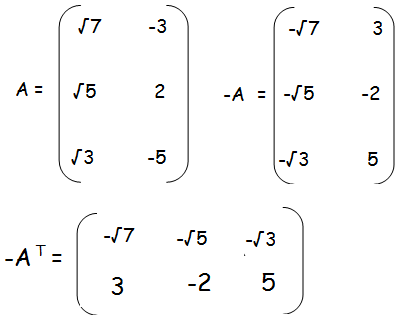
Question 3 :

If A =

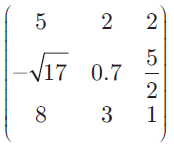
then verify (A^T )^T = A.

Solution :

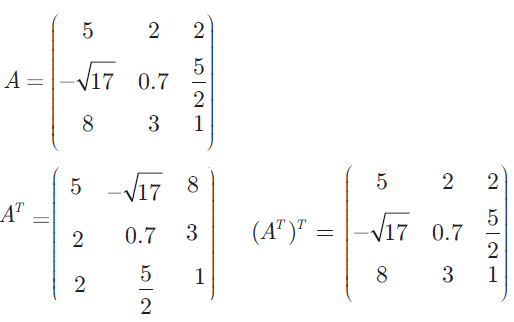
Hence proved.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

HOW TO FIND THE TRANSPOSE OF A MATRIX

Recent Articles

Best Way to Learn Mathematics

SAT Math Videos (Part - 1)

SAT Math Resources (Videos, Concepts, Worksheets and More)