HOW TO FIND THE SLOPE OF A LINE

Methods to Find the Slope of a Line

Method 1 :

The formula for slope is referred to rise over run,

Because the fraction consists of the rise (the change in y, going up or down) divided by the run (the change in x, going from left to the right).

The diagram shown below illustrates this.

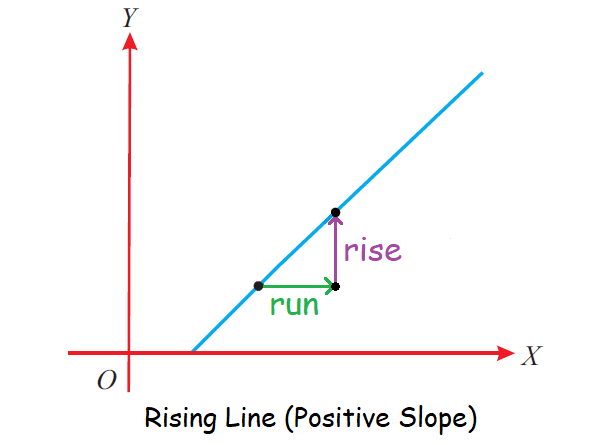
The simplest way to look at the slope is

rise/run

(rise over run)

In the formula (rise / run), we can "rise" up or down... but, we ALWAYS "run" to the right.

Method 2 :

If a straight line is passing through the two points (x₁, y₁) and (x₂, y₂), then the formula to find the slope of the line is

m = (y₂ - y₁)/(x₂ - x₁)

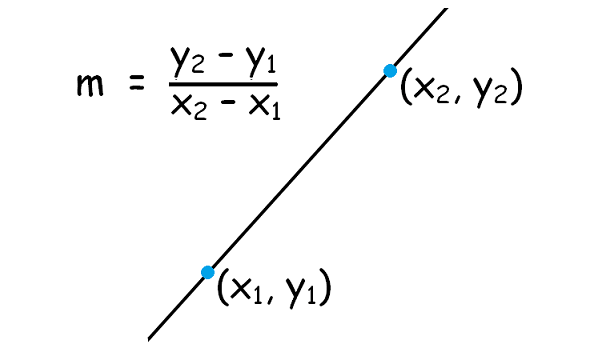
Method 3 :

Let θ be the angle between the straight line "l" and the positive side of x - axis.

The figure given below illustrates this.

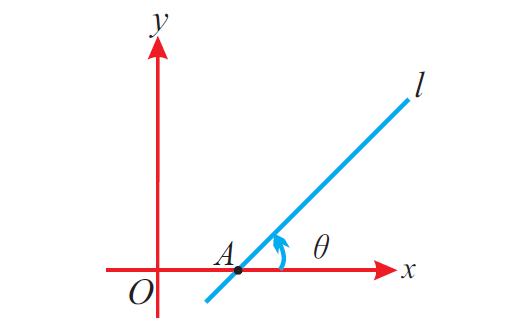
Then, the formula to find slope of the line is

m = tan θ

Method 4 :

If the equation of a straight line given in general form or standard form

ax + by + c = 0 / ax + by = c

then write the given equation in slope-intercept form

y = mx + b,

where m is the slope and b is the y-intercept.

Once you write the equation in slope-intercept form, the coefficient of x (m) on the right side of the equation is the slope of the line.

Slope of a Line - Positive or Negative or Zero or Undefined

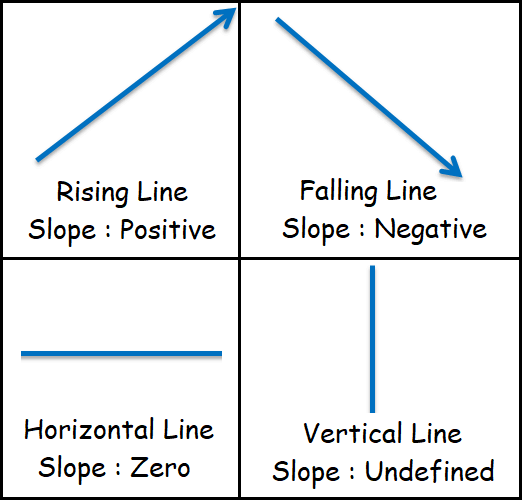
To know the sign of the slope of a straight line, always we have to look at the straight line from left to right.

(i) If the line is going (from left to right) towards up, then the line is called rising line and its slope will be a positive value.

(ii) If the line is going (from left to right) towards down, then the line is called falling line and its slope will be a negative value.

(iii) If the line is horizontal, the slope will be zero.

(iv) If the line is vertical, the slope will be undefined.

Solving Problems on Slope of a Line

Problem 1 :

What is the slope of a line whose inclination with positive direction of x -axis is (i) 90° (ii) 0.

Solution :

(i) θ = 90°

m = tanθ

= tan90°

  = undefined

(i) θ = 0°

m = tanθ

= tan 0°

  = 0

Problem 2 :

What is the inclination of a line whose slope is (i) 0 (ii) 1.

Solution :

(i) 0

m = 0

tanθ = 0

θ = tan^-1(0)

θ = 0°

Hence the required angle of inclination is 0°.

(ii) 1

m = 1

tanθ = 1

θ = tan^-1(1)

θ = 45°

Hence the required angle of inclination is 45°.

Problem 3 :

Find the slope of a line joining the points

(i) (5, 5) with the origin

Solution :

m = (y₂ - y₁)/(x₂ - x₁)

Substitute x₁ = 5, x₂ = 0, y₁ = 5 and y₂ = 0.

m = (0 - 5)/(0 - 5)

= -5/(-5)

= 1

(ii) (sin θ, -cos θ) and (-sin θ , cos θ)

Solution :

Substitute x₁ = sinθ, x₂ =-sinθ, y₁ = -cosθ and y₂ = cosθ.

m = (cosθ - (-cosθ))/(-sinθ - sinθ)

= (cosθ + cosθ)/(-sinθ - sinθ)

= (2cosθ)/(-2sinθ)

= -cosθ/sinθ

= -cotθ

Problem 4 :

What is the slope of a line perpendicular to the line joining A(5, 1) and P where P is the mid-point of the segment joining (4,2) and (-6, 4).

Solution :

P is the mid-point of the segment joining (4,2) and (-6, 4).

First, let us find the point P.

midpoint = ((x₁ + x₂)/2, (y₁ + y₂)/2)

= ((4 - 6)/2, (2 + 4)/2)

= (-2/2, 6/2)

 = P(-1, 3)

Now, we have to find the slope of the line which is perpendicular to the line joining the points A(5, 1) and P(-1, 3).

Slope of AP x slope of the required line = -1.

Slope of AP = (y₂ - y₁)/(x₂ - x₁)

= (3 - 1)/(-1 - 5)

= 2/(-6)

  = -1/3

Slope of the required line = -1/(-1/3).

= 3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.