HOW TO FIND THE ROOTS OF A POLYNOMIAL OF DEGREE 4
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Example 1 :
Solve the equation
x4+4x3+5x2+2x-2 = 0
which one root is -1 + i
Solution :
Let
f(x) = x4 + 4x3 + 5x2 + 2x - 2
Since one of the root is complex number, the other root may be its conjugate.
So, α = -1 + i β = - 1 - i
By using these two roots we can find a quadratic equation which is the part of the original equation. First, let us find the quadratic equation.
General form of any quadratic equation:
x²-(α+β)x+αβ = 0
α = -1+i β = -1-i
Sum of roots (α+β) = -1+i-1-i
= - 2
Product of roots (αβ) = (-1+i) (-1-i)
= (-1)2 - i2
= 2
Therefore the required quadratic equation
x2-(-2)x+2 = 0
x²+2x+2 = 0
This is the part of the equation of polynomial of degree 4.
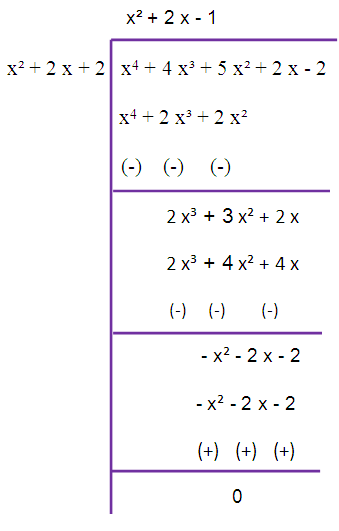
By solving this quadratic equation
x2+2x-1 = 0
we get other two roots.
a = 1, b = 2, c = -1
x = [- b ± √(b2-4 a c)]/2 a
x = [-2 ± √(22-4 (1)(-1))]/2 (1)
x = [- 2 ± √8]/2
x = [- 2 ± 2 √2]/2
x = -1±√2
Therefore the four roots are
-1 + i ,- 1 - i , - 1 + √2 , - 1 - √2.
Example 2 :
Solve the equation
6x4 − 35x3 + 62x2 − 35x + 6 = 0
Solution :
By suing synthetic division repeatedly, we may solve this problem.
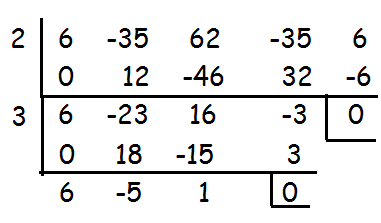
2 and 3 are the solutions of the given polynomial. To know the other solutions, let us solve the quadratic equation.
6x2 - 5x + 1 = 0
6x2 - 2x - 3x + 1 = 0
2x (3x - 1) - 1(3x - 1) = 0
(2x - 1) (3x - 1) = 0
2x - 1 = 0 and 3x - 1 = 0
x = 1/2 and x = 1/3
Hence the solutions are 2, 3, 1/2 and 1/3
Example 3 :
Solve
x4 + 3x3 - 3x - 1 = 0
Solution :
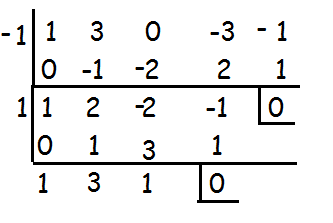
1 and -1 are the solutions of the given polynomial, to find other two solutions, let us solve the quadratic equation
x2 + 3x + 1 = 0
x = -b ± √(b2 - 4ac) / 2a
x = -3 ± √(9 - 4) / 2(1)
x = (-3 ± √5)/2
So, roots are -1, 1, (-3 ± √5)/2.
Example 4 :
Solve the equation 6x4 − 5x3 − 38x2 − 5x + 6 = 0 if it is known that 1/3 is a solution.
Solution :
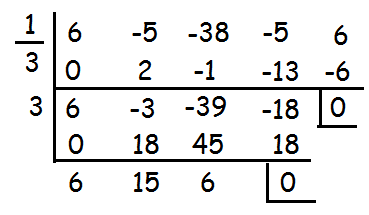
1/3 and 3 are solutions of the given polynomial, to find other two solutions, let us solve the quadratic equation.
6x2 + 15x + 6 = 0
6x2 + 12x + 3x + 6 = 0
6x(x + 2) + 3(x + 2) = 0
(6x + 3)(x + 2) = 0
x = -1/2 and x = -2
Hence the solutions are -1/2, -2, 3 and 1/3.
Example 5 :
Solve the equation x4 −14x2 + 45 = 0
Solution :
Let x2 = t
t2 − 14t + 45 = 0
t2 − 9t - 5t + 45 = 0
t(t - 9) - 5(t - 9) = 0
(t - 5) (t - 9) = 0
t = 5 and t = 9
x2 = 5, x2 = 9
x = ±√5, x = ±3
Hence the solutions are √5, -√5, 3 and -3.
I can find the roots of a given polynomial using factoring. Factor each polynomial and state the roots.
Example 6 :
x4 - 3x3 - 4x2 = 0
Solution :
x4 - 3x3 - 4x2 = 0
x2 (x2 - 3x - 4 ) = 0
x2 (x - 4)(x + 1) = 0
x2 = 0, x - 4 = 0 and x + 1 = 0
x = 0, x = 4 and x = -1
So, the roots are -1, 0 and 4.
Example 7 :
x3 + 3x2 - x - 3 = 0
Solution :
x3 + 3x2 - x - 3 = 0
x2 (x + 3) - 1 (x + 3) = 0
(x2 - 1)(x + 3)= 0
x2 - 1 = 0, x + 3 = 0
x2 = 1, x = -3
x = √1 and x = -3
x = ± 1 and x = -3
So, the roots are -1, -3, 1.
Example 8 :
x4 + 5x3 - x2 - 5x = 0
Solution :
x4 + 5x3 - x2 - 5x = 0
Factoring x, we get
x(x3 + 5x2 - x - 5) = 0
Using grouping method, we get
x[x2 (x + 5) - 1(x + 5)] = 0
x(x2 - 1)(x + 5) = 0
Equating each factor to 0, we get
|
x = 0 |
x2 - 1 = 0 x2 = 1 x = ±1 x = -1 and 1 |
x + 5 = 0 x = -5 |
So, the solutions are -5, -1, 0 and 1.
Example 9 :
x4 - 10x2 + 9 = 0
Solution :
Let x2 = t
(x2)2 - 10x2 + 9 = 0
t2 - 10t + 9 = 0
(t - 9)(t - 1) = 0
Equating each factor to 0, we get
t = 9 and t = 1
Applying the value of t, we get
x2 = 9 and x2 = 1
x = ±3 and x = ±1
x = -3, -1, 1 and 3.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 50)
Mar 06, 26 07:48 PM
Digital SAT Math Problems and Solutions (Part - 50) -
Digital SAT Math Problems and Solutions (Part - 49)
Mar 06, 26 06:47 PM
Digital SAT Math Problems and Solutions (Part - 49) -
Digital SAT Math Problems and Solutions (Part - 48)
Mar 06, 26 05:24 PM
Digital SAT Math Problems and Solutions (Part - 48)


