HOW TO FIND THE MISSING VERTEX OF A TRIANGLE WHEN CENTROID IS GIVEN

A centroid of a triangle is the point where the three medians of the triangle meet. A median of a triangle is a line segment from one vertex to the mid point on the opposite side of the triangle. 

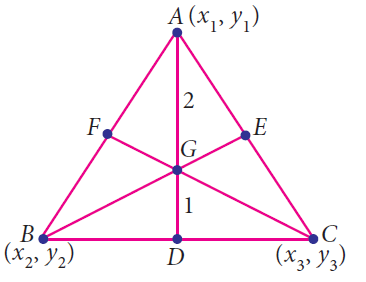
The centroid G of the triangle with vertices A(x₁, y₁), B(x₂ , y₂ ) and C(x₃ , y₃) is

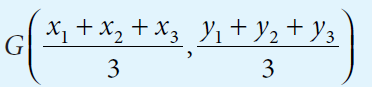
Let us look at some examples to understand how to find the missing vertex of a triangle when centroid is given

Example 1 :

Find the missing vertex of triangle whose two of the vertices are (0, 0), (-8, 0) and centroid is (-5, -2).

Solution :

Centroid of a triangle = (x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3

Let the required vertex be C (a, b)

A(0, 0) B(-8, 0) and C (a, b)

x₁  =  0, x₂  =  -8, x₃  =  a

y₁  =  0, y₂  =  0, y₃  =  b

(0 - 8 + a)/3 , (0 + 0 + b)/3  =  (-5, -2)

(-8 + a)/3 , b/3  =  (-5, -2)

Equating the x and y coordinates, we get

So the required vertex be (-7, -6).

Example 2 :

The centroid of a triangle ABC is (1, 1). Two of the vertices are A (3, -4), B (-4, 7). Find the coordinates of the third vertex.

Solution :

Centroid of a triangle = (x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3

Let the required vertex be C (a, b)

A (3, -4), B (-4, 7) and C (a, b)

x₁  =  3, x₂  =  -4, x₃  =  a

y₁  =  -4, y₂  =  7, y₃  =  b

(3 - 4 + a)/3 , (-4 + 7 + b)/3  =  (1, 1)

(-1 + a)/3 , b/3  =  (1, 1)

Equating the x and y coordinates, we get

Hence the required vertex is (4, 3).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.