HOW TO FIND THE MISSING DIGIT

Examples 1-8 : Find the missing digit.

Example 1 :

Solution :

From the above calculation, the missing digit is 7.

Example 2 :

Solution :

From the above calculation, the missing digit is 3.

Example 3 :

Solution :

From the above calculation, the missing digit is 9.

Example 4 :

Solution :

From the above calculation, the missing digit is 7.

Example 5 :

Solution :

From the above calculation, the missing digit is 8.

Example 6 :

Solution :

From the above calculation, the missing digit is 8.

Example 7 :

Solution :

From the above calculation, the missing digit is 4.

Example 8 :

Solution :

From the above calculation, the missing digit is 1.

Example 9 :

In the product given below, if 2y is a two digit number, find the value of y.

(2y)(12) = 348

Solution :

(2y)(12) = 348 ----(1)

The digit in ones place of 288 is 8.

In 2y and 12, the product of the digits in once place (y and 2) will produce the digit in ones place of the resulting number 288, that is 8.

So, the value of y can be 4 or 9.

Because,

4 x 2 = 8

9 x 2 = 18

Substitute y = 4 in (1).

(24)(12) = 288

(y = 4 doesn't work)

Substitute y = 9 in (1).

(29)(12) = 348

(y = 9 works)

Therefore the value of y is 9.

Example 10 :

If the following number is evenly divisible by 3, find the least possible value of K such that K > 0.

3K4591

Solution :

According to divisibility rule, if a number is evenly divisible by 3, the digits in the number will add up to a multiple of 3.

Add the digits in the given number 3K4591.

3 + K + 4 + 5 + 9 + 1 = 22 + K

If k = 2,

22 + k = 24 ----> multiple of 3

If k = 5,

22 + k = 27 ----> multiple of 3

If k = 8,

22 + k = 30 ----> multiple of 3

Therefore, the least possible value of k is 2.

Example 11 :

Write in the missing digit:

4__ x 7 = 301

Solution :

4__ x 7 = 301

By observing the question, we understand that the first number is two digit number.

The unit digit of the answer is 1.

To find the missing digit, we should have a logical thinking that, multiplying 7 by what we get the number ends with 1.

3 x 7 = 21 (ends with 1)

43 x 7 = 301

So, the missing digits is 7.

Example 12 :

Write in the missing digit:

__ 2 x 6 = 192

Solution :

__2 x 6 = 192

By observing the question, we understand that the first number is two digit number.

By multiplying 2 and 6, we get 12 in which we write 2 and 1 as remainder.

When the missing digit is fixed as 3, then

32 x 6 = 192

When the missing digit is fixed as 4, then the result will end with 2 but it must be greater than 192. 

So, the missing digit is 3.

Example 12 :

Write in the missing digit:

28 x __ __ = 280

Solution :

28 x __ __ = 280

The missing digits will create a two digit number, since the result ends with 0 the missing number may be 10. 

28 x 10 = 280

So, the missing two digit number is 10.

Write in the missing digits in these division questions. None of the sums has a remainder.

Example 13 :

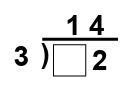
Solution :

Division algorithm,

dividend = divisor x quotient + remainder.

Here the remainder is 0 since there is no remainder.

Dividend = __ 2, divisor = 3, quotient = 14 and remainder = 0

__2 = 3 x 14 + 0

__2 = 42 + 0

__2 = 42

So, the missing digit is 4.

Example 14 :

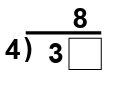
Solution :

Dividend = 3__, divisor = 4, quotient = 8 and remainder = 0

3__ = 4 x 8 + 0

3__ = 32 + 0

3__ = 32

So, the missing digit is 2.

Example 15 :

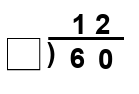
Solution :

Dividend = 3__, divisor = 4, quotient = 8 and remainder = 0

3__ = 4 x 8 + 0

3__ = 32 + 0

3__ = 32

So, the missing digit is 2.

Example 16 :

What are the values of A, B, C and D in the following question?

a) A = 3, B = 6, C = 5 and D = 2

b) A = 4, B = 5, C = 0 and D = 3

c) A = 5, B = 3, C = 4 and D = 1

d) A = 6, B = 9, C = 2 and D = 4

Solution :

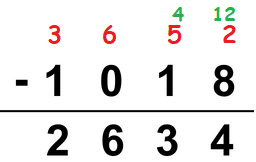
So, option a is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.