HOW TO FIND THE MISSING COORDINATE IN A PARALLELOGRAM

To find the missing coordinate of a parallelogram, we use one of the following methods.

(i) Using slope

(ii) Using midpoint formula

(iii) Using section formula

How to find the missing coordinate of a parallelogram using slope ?

In a parallelogram, the opposite sides are parallel. If two lines are parallel, then its slopes will be equal.

Let us consider the parallelogram ABCD,

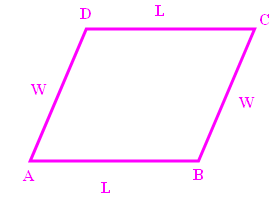
Slope of AB  =  Slope of CD

Slope of BC  =  Slope of AD

How to find the missing coordinate of a parallelogram using midpoint formula ?

In a parallelogram, the diagonals will bisect each other.

That is, the midpoint of one diagonal is also the midpoint of another diagonal. 

Let us consider the parallelogram ABCD,

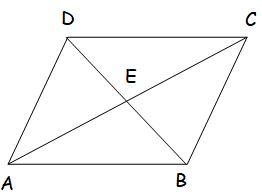
Midpoint of AC  =  Midpoint of BD

How to find missing coordinate of parallelogram using section formula ?

The point of intersection of diagonals divides the diagonals in the same ratio.

For example, if the the common point of both diagonals is in the ratio l : m, then the value of l and m are equal.

Let us look at some examples to understand the above explained concepts.

Example 1 :

If (7, 3), (6, 1), (8, 2) and (p, 4) are the vertices of a parallelogram taken in order, then find the value of p.

Solution :

Let the vertices of the parallelogram be A (7, 3), B(6, 1), C (8, 2) and D (p, 4)

We know that the diagonals of a parallelogram bisect each other. The midpoints of the diagonal AC and the diagonal BD coincide.

Midpoint of AC  =  Midpoint of BD

Midpoint  =  (x₁ + x₂)/2 ,  (y₁ + y₂)/2

A (7, 3) and C (8, 2)

=  (7 + 8)/2 , (3 + 2)/2

=  (15/2, 5/2)  ---------(1)

B (6, 1) and D (p, 4) 

  =  (6 + p)/2 , (1 + 4)/2

=  (6 + p)/2 , 5/2  ---------(2)

(15/2, 5/2)  =  ((6 + p)/2 , 5/2)

Equating x-coordinates, we get

15/2  =  (6 + P) / 2

15  =  6 + p

Subtract 6 on both sides,

15 - 6  = 6 + p - 6

9  =  p

So, the missing coordinate is 9.

Example 2 :

Using the concept of slope, find the missing coordinate (-2 , -1), (4 , 0), (a , 3) and (-3 , 2) taken in order form a parallelogram.

Solution :

Let the vertices of the parallelogram be A (-2 , -1), B (4 , 0), C (a , 3) and D (-3 , 2)

Slope of AB  =  Slope of CD

Slope  =  (y₂- y₁) / (x₂-x₁)

Slope of AB : 

A (-2 , -1), B (4 , 0)

  m  =  (0 - (-1)) / (4 - (-2))

  m  =  (0 + 1) / (4 + 2)

  m  =  1 / 6  ------(1)  

Slope of CD : 

 C (a , 3) and D (-3 , 2)

  m  =  (2 - 3) / (-3 - a)

  m  =  - 1 / (-3 - a)

  m  =  1 / (3 + a) ------(2)

1/6  =  1/(3 + a)

3 + a  =  6

Subtract 3 on both sides

3 + a - 3  =  6 - 3

a  =  3

So, the missing coordinate is 3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.