HOW TO FIND THE LEAST NUMBER TO BE SUBTRACTED TO GET A PERFECT SQUARE

Example 1 :

Find the least number which must be subtracted from 104979 so as to get a perfect square.

Solution :

Find the square root of 104979 using long division method.

Step 1 :

Separate the digits by taking commas from right to left once in two digits.

10,49,79

When we do so, we get 10 before the first comma.

Step 2 :

Now we have to multiply a number by itself such that

the product ≤ 10

(The product must be greatest and also less than 10)

The above condition will be met by '3'.

Because 3 ⋅ 3 = 9 ≤ 10.

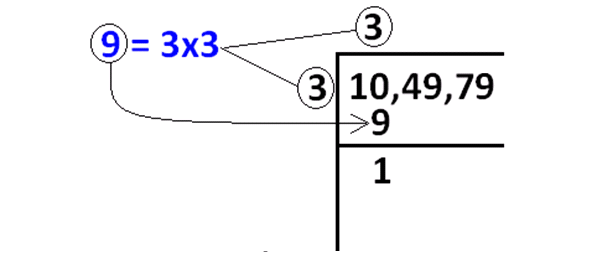
In the above picture, 9 is subtracted from 10 and we got the remainder 1.

Step 3 :

Now, we have to bring down 49 and quotient 3 to be multiplied by 2 as given in the picture below.

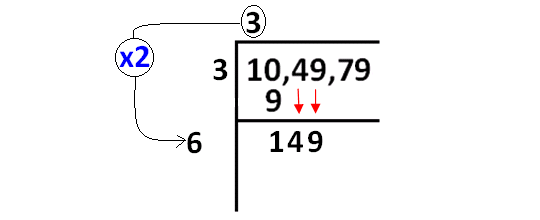
Step 4 :

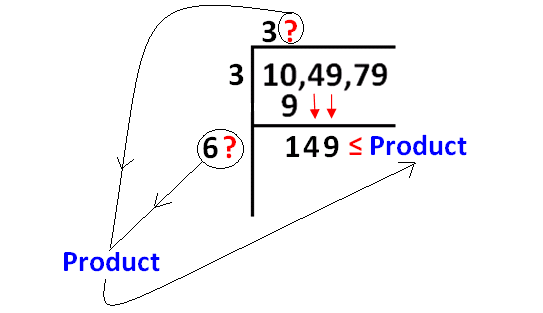
Now we have to take a same number at the two places indicated by '?'.

Then, we have to find the product as shown in the picture and also the product must meet the condition as indicated.

Step 5 :

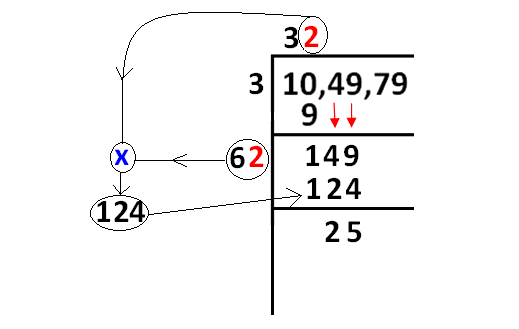
The condition said in step 4 will be met by replacing '?' with '2'.

Than we have to do the calculation as given in the picture.

Step 6 :

Now, we have to bring down 79 and quotient 32 to be multiplied by 2 as given in the picture below.

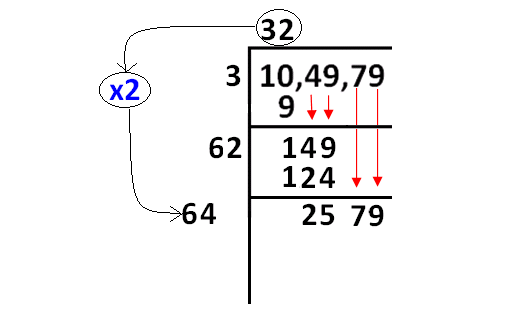
Step 7 :

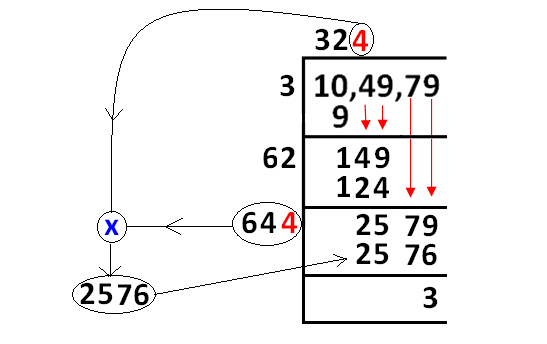
In finding square root of 104979 using long division, we obtain the remainder 3.

If the given number is a perfect square, then we would have obtained the remainder zero.

Since we obtain the remainder 3 (≠ 0), 104979 is not a perfect square. To get a perfect square, we have to subtract 3 from 104979.

104979 - 3 = 104976

Thus,

√104976 = 324

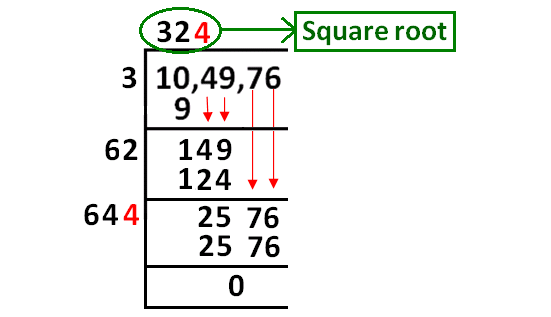
Therefore, 3 is the least number which must be subtracted from 104979 so as to get a perfect square.

Example 2 :

Find the least number which must be subtracted from 1989 so as to get a perfect square.

Solution :

Find the square root of 1989 using long division method.

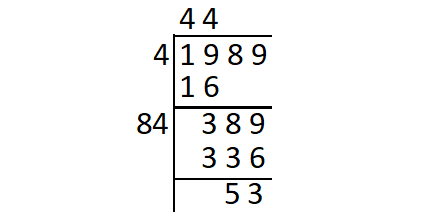
So, 53 is the least number which must be subtracted from 1989 so as to get a perfect square.

1989 - 53 = 1936

Thus,

√1936 = 44

Example 3 :

Find the least number which must be subtracted from 3250 so as to get a perfect square.

Solution :

Find the square root of 3250 using long division method.

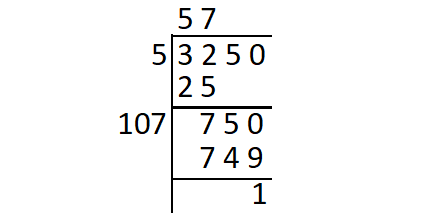
So, 1 is the least number which must be subtracted from 3250 so as to get a perfect square.

3250 - 1 = 3249

Thus,

√3249 = 57

Example 4 :

Find the least number which must be subtracted from 4000 so as to get a perfect square.

Solution :

Find the square root of 4000 using long division method.

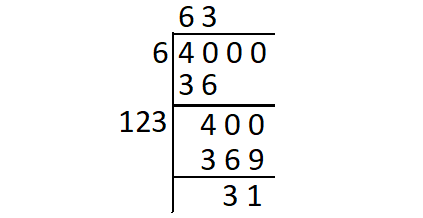
So, 31 is the least number which must be subtracted from 4000 so as to get a perfect square.

4000 - 31 = 3969

Thus,

√3969 = 63

Example 5 :

What is the smallest number to be subtracted from 549162 in order to make it perfect square ?

Solution :

Finding the square root of 549162, we get

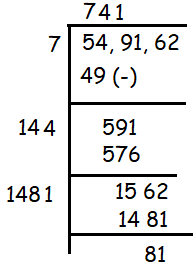
741 x 741 = 549081

849162 - 549081 ==> 81

So, 81 is the smallest number should be subtracted with 549162 to make it as perfect square.

Example 6 :

What is the least number which should be subtracted from 0.000326 to make it a perfect square ?

Solution :

Given number is 0.000326

Multiplying both numerator and denominator by 1000000.

= 0.000326 x (1000000/1000000)

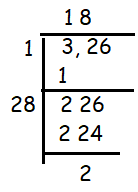
18² = 324

19² = 361

326 - 324 ==> 2/1000000

= 0.000002

So, 0.000002 is the number to be subtracted to make it as a perfect square.

Example 7 :

Find the least number that must be subtracted from 5607 so as to get a perfect square. Also find the square root of the perfect square.

Solution :

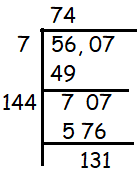
74 x 74 = 5476

= 5607 - 5476

= 131

So, the required number to be subtracted from the given number is 131.

After subtracting 131 from 5607, we get 5476 and square root of 5476 is 74.

Example 8 :

Find the least number that must be subtracted from 402 so as to get a perfect square. Also find the square root of the perfect square.

Solution :

402 is not a perfect square, to make the given number as perfect square we have to subtract 2 from 402. Then we get 400.

Square root of 400 is 20.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.