HOW TO FIND THE LEAST COMMON MULTIPLE

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

The the smallest value among the common multiples of two or more numbers is called their least common multiple (LCM).

We can use the following methods to find least common multiple of the given numbers

(i) Prime Factorization Method

(ii) Division Method

Prime Factorization Method

The following steps would be useful to find the least common multiple of the given numbers using prime factorization.

Step 1 :

Find the prime factors of the given numbers

Step 2 :

Take each prime factor with its maximum times of repetitions.

Step 3 :

Multiply all the prime factors in step 2 to get the least common multiple of the given numbers.

Example 1 :

Find the least common multiple of 24 and 60 using prime factorization method.

Solution :

Resolve the given numbers into their prime factors as shown below.

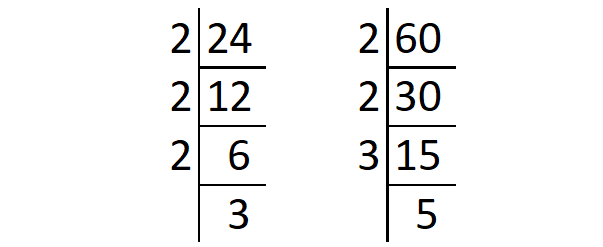
From the above division,

24 = 2 x 2 x 2 x 3

60 = 2 x 2 x 3 x 5

The different prime factors are 2, 3 and 5.

The prime factor 2 appears a maximum of 3 times in the prime factorization of 24.

The prime factor 3 appears a maximum of 1 time in the prime factorization of both 24 and 60.

The prime factor 5 appears a maximum of 1 time in the prime factorization of 60.

Therefore, the least common multiple of 24 and 60 is

= 2 x 2 x 2 x 3 x 5

= 120

Example 2 :

Find the least common multiple of 48, 72 and 108 using prime factorization method.

Solution :

Resolve the given numbers into their prime factors as shown below.

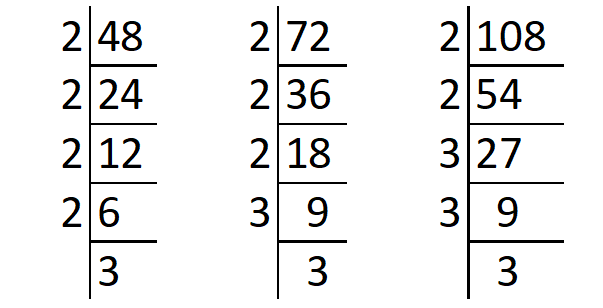
From the above division,

48 = 2 x 2 x 2 x 2 x 3

72 = 2 x 2 x 2 x 3 x 3

108 = 2 x 2 x 3 x 3 x 3

The different prime factors are 2 and 3

The prime factor 2 appears a maximum of 4 times in the prime factorization of 48.

The prime factor 3 appears a maximum of 3 times in the prime factorization of 108.

Therefore, the least common multiple of 48, 72 and 108 is

= 2 x 2 x 2 x 2 x 3 x 3 x 3

= 432

Division Method

Finding the least common multiple of two numbers :

Using L division, divide both the numbers by a common divisor.

Continue this process, until you get a common divisor for both the numbers.

At one stage, there will be no common divisor for both the numbers.

Then, multiply all the common divisors and the numbers at the last stage to get the least common multiple of the given two numbers.

Note :

Usually prime numbers are being used as divisors.

Example 3 :

Find the least common multiple of 24 and 60 using division method.

Solution :

Using L division, divide both the numbers by a common divisor. Continue this process, until you get a common divisor for both the numbers.

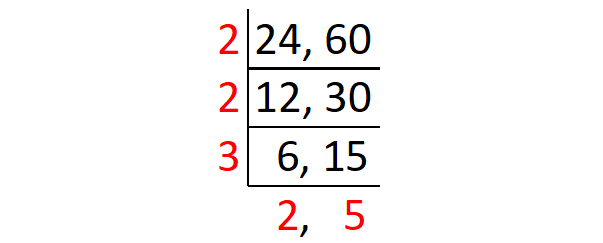
The least common multiple of 24 and 60 is

= 2 x 2 x 3 x 2 x 5

= 120

Finding the least common multiple for more than two numbers :

Consider the least common multiple of three numbers.

Try to get a common divisor for all the given three numbers.

If you get a common divisor for all the three numbers, using L division, divide all the the three numbers by it.

If you don't get a common divisor for all the three numbers, try to get a common divisor for at least two numbers and divide those two numbers by it. Write the third number as it is.

Continue this process, until you get a common divisor for at least two numbers.

At one stage, there will be no common divisor even for two numbers.

Then, multiply all the common divisors and the numbers at the last stage to get the least common multiple of the given three numbers.

You can follow the same process to find the least common multiple for than three numbers.

Example 4 :

Find the least common multiple of 48, 72 and 108 using division method.

Solution :

Using L division, divide the given numbers by a common divisor. Continue this process, until you get a common divisor at least for any of the two numbers.

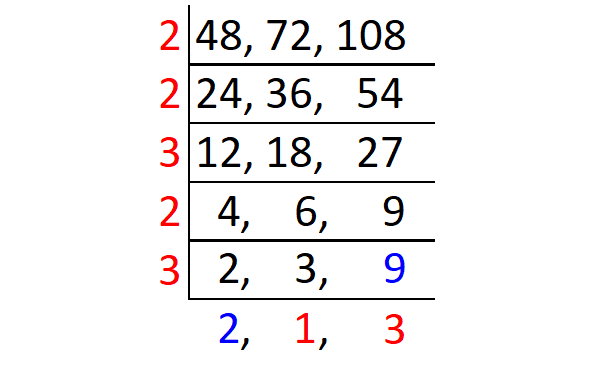
The least common multiple of 48, 72 and 108 is

= 2 x 2 x 3 x 2 x 3 x 2 x 1 x 3

= 432

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

About Us | Contact Us | Privacy Policy

HOW TO FIND THE LEAST COMMON MULTIPLE

Prime Factorization Method

Division Method

Recent Articles

10 Hard SAT Math Questions (Part - 43)

90 Degree Clockwise Rotation

US Common Core K-12 Curriculum Algebra Solving Systems of Equations