HOW TO FIND THE AREA OF THE SECTOR
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Area of a sector is the region bounded by the bounding radii and the arc of the sector.
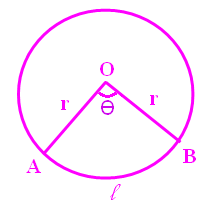
There are two methods to find the area of a sector.
(i) when the central angle and the radius are given
(ii) when length of arc and the radius are given
Area of a sector :
= (θ/360) ⋅ πr2 square units
(or)
= (lr/2) square units
θ - central angle formed by the sector
L - length of arc
r - radius of the sector
We can use the first formula if the central angle(θ) formed by the sector and radius are given. If the length of arc(L) are given, we have to use the second formula.
Area of Sector When Angle and Radius are Given
Example 1 :
Find the area of the sector whose radius and central angle are 42 cm and 60° respectively.
Solution :
Area of the sector :
= (θ/360°) ⋅ πr2
Substitute r = 42 cm , θ = 60°.
= (60°/360°) ⋅ π ⋅ 422
= (60°/360°) ⋅ π ⋅ 42 ⋅ 42
= (1/6) ⋅ π ⋅ 42 ⋅ 42
= 294π cm2
Example 2 :
Find the area of the sector whose radius and central angle are 21 cm and 60° respectively.
Solution:
Area of the sector :
= (θ/360°) ⋅ πr2
Substitute r = 21 cm , θ = 60°.
= (60°/360°) ⋅ π ⋅ 212
= (1/6) ⋅ π ⋅ 21 ⋅ 21
= 73.5π cm2
Example 3 :
Find the area of the sector whose radius and central angle are 4.9 cm and 30° respectively.
Solution :
Area of the sector :
= (θ/360°) ⋅ πr2
Substitute r = 4.9 cm , θ = 30°.
= (30°/360°) ⋅ π ⋅ 4.92
= (1/12) ⋅ π ⋅ 4.9 ⋅ 4.9
≈ 73.5π cm2
Area of Sector When Length of Arc and Radius are Given
Example 4 :
Find the area of the sector and also find the central angle formed by the sector whose radius is 21 cm and length of arc is 66 cm (Use π ≈ 22/7).
Solution :
Area of the sector :
= (lr/2) square units
Substitute l = 66 and r = 21.
= (66 ⋅ 21)/2
= 693 cm2
Central angle formed by the sector :
Area of sector = 693 cm2
(θ/360)⋅ πr2 = 693
Substitute the known values and solve for θ.
(θ/360)⋅ (22/7)(21)2 = 693
1386θ/360 = 693
77θ/20 = 693
Multiply each side by 20/77.
θ = 180°
Example 5 :
Find the area of the sector whose radius and length of arc are 6 cm and 20 cm.
Solution :
Area of the sector :
= (lr/2) square units
Substitute l = 6 and r = 20.
= (6 ⋅ 20)/2
= 60 cm2
Example 6 :
Find the area of the sector whose diameter and length of arc are 10 cm and 40 cm respectively.
Solution :
Radius = Diameter /2
= 10/2
= 5 cm
Area of the sector :
= (lr/2) square units
Substitute l = 40 and r = 5.
= (40 ⋅ 5)/2
= 100 cm2
How to Find the Area From the Given Perimeter
Example 7 :
Find the area of the sector whose radius is 35 cm and perimeter is 147 cm.
Solution :

Perimeter of sector = 147 cm
l + 2r = 147
l + 2(35) = 147
l + 70 = 147
l = 77 cm
Area of the sector :
= (lr)/2 square units
Substitute l = 77 and r = 35.
= (77 ⋅ 35)/2
= 1347.5 cm2
Example 8 :
Find the area of the sector whose radius is 20 cm and perimeter is 110 cm.
Solution :
Perimeter of sector = 110 cm
l + 2r = 110
l + 2(20) = 110
l + 40 = 110
l = 70 cm
Area of the sector :
= (lr)/2 square units
Substitute l = 70 and r = 20.
= (70 ⋅ 20)/2
= 700 cm2
Example 8 :
In a xy plane below, O is the center of circle and the measure of <AOD is π/3. If the radius of circle O is 6, what is the length of AD ?
a) 3 b) 3√2 c) 4.5 d) 3√3

Solution :
<AOD = π/3
Radius of the circle = OA
sin θ = Opposite side / Hypotenuse
sin π/3 = AD / OA
√3/2 = AD / 6
AD = (√3/2) x 6
AD = 3√3
Example 9 :
In the xy-plane above, O is the center of the circle, and the measure of <POQ is kπ radians. What is the value of k ?

Solution :
<POQ = kπ

tan θ = Opposite side / Adjacent side
tan kπ = 1/1
tan kπ = 1
kπ = tan-1(1)
kπ = π/4
So, the value of k is 1/4.
Example 10 :
In the -xy plane above, O is the center of the circle, and the measure of ∠POQ is a degree.

Solution :

tan θ = Opposite side / Adjacent side
tan (180 - a) = -√3/1
(180 - a) = tan-1(-√3)
(180 - a) = 120
a = 180 - 120
a = 60
So, the value of a is 60 degree.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus BC Problems with Solutions
Dec 20, 25 10:51 AM
AP Calculus BC Problems with Solutions -
AP Precalculus Problems and Solutions (Part - 1)
Dec 20, 25 10:49 AM
AP Precalculus Problems and Solutions (Part - 1) -
AP Calculus AB Problems with Solutions (Part - 1)
Dec 20, 25 10:49 AM
AP Calculus AB Problems with Solutions (Part - 1)
