HOW TO FIND THE AREA OF A RHOMBUS WITH VERTICES

Let d₁ and d₂ be the lengths of the diagonals of a rhombus.

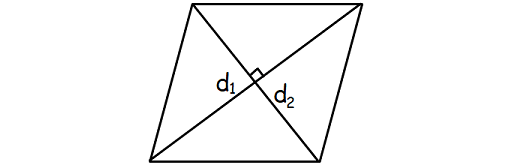
Formula for area of a rhombus :

If the four vertices of a rhombus are given, find the length of each diagonal using distance formula and find the area of the rhombus using the formula given above.

Distance between the two points (x₁, y₁) and (x₂, y₂) :

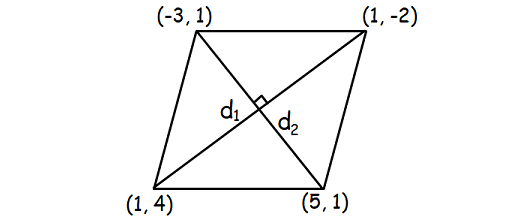
Example 1 :

Find the area of a rhombus with the following vertices taken in order.

(1, 4), (5, 1), (1, -2), (-3, 1)

Solution :

Length of of diagonal d₁ :

d₁ = √[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁) = (1, 4) and (x₂, y₂) = (1, -2).

d₁ = √[(1 - 1)² + (-2 - 4)²]

= √[0 + (-6)²]

= √36

= 6

Length of of diagonal d₂ :

d₂ = √[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁) = (5, 1) and (x₂, y₂) = (-3, 1).

d₂ = √[(-3 - 5)² + (1 - 1)²]

= √[(-8)² + 0]

= √64

= 8

Area of rhombus :

= (1/2) x d₁ x d₂

Substitute d₁ = 8 and d₂ = 6.

= (1/2) x 8 x 6

= 24 square units

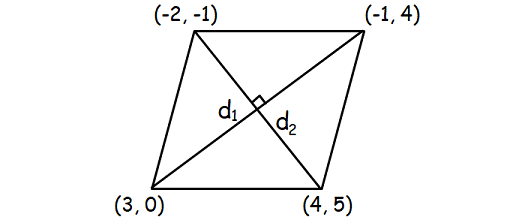
Example 2 :

Find the area of a rhombus with the following vertices taken in order.

(3, 0), (4, 5), (-1, 4), (-2, -1)

Solution :

Length of of diagonal d₁ :

d₁ = √[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁) = (3, 0) and (x₂, y₂) = (-1, 4).

d₁ = √[(-1 - 3)² + (4 - 0)²]

= √[(-4)² + 4²]

= √[16 + 16]

= √32

= √(2 x 16)

= 4√2

Length of of diagonal d₂ :

d₂ = √[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁) = (4, 5) and (x₂, y₂) = (-2, -1).

d₂ = √[(-2 - 4)² + (-1 - 5)²]

= √[(-6)² + (-6)²]

= √[36 + 36]

= √72

= √(2 x 36)

= 6√2

Area of rhombus :

= (1/2) x d₁ x d₂

Substitute d₁ = 4√2 and d₂ = 6√2.

= (1/2) x 4√2 x 6√2

= 24 square units

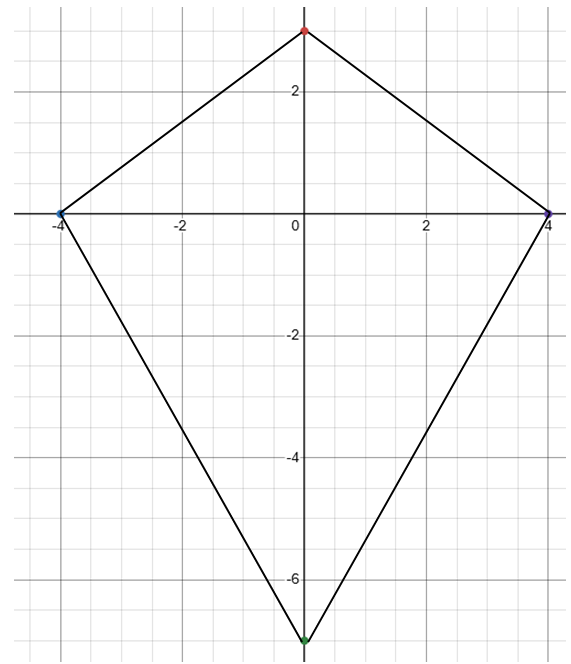
Example 3 :

Kite CHSR has vertices at C(0, 3), H(-4, 0) S (0, -7) and R(4, 0). Find the area of kite CHSR.

Solution :

Distance between (-4, 0) and (4, 0) :

d₁ = √[(x₂ - x₁)² + (y₂ - y₁)²]

= √[(4 + 4)² + (0 - 0)²]

= √8² + 0

= 8

Distance between (0, 3) and (0, -7) :

d₂ = √[(x₂ - x₁)² + (y₂ - y₁)²]

= √[(0 - 0)² + (-7 - 3)²]

= √0² + (-10)²

= 10

Area of kite = (1/2) x 8 x 10

= 4 x 10

= 40 square units.

Example 4 :

The area of rhombus is 84 sq.cm and the length of one diagonal is 24 cm. The length of the other diagonal is 

Solution :

Area of rhombus = 84 sq.cm

Length of one diagonal (d₁) = 24 cm

Length of other diagonal (d₂) = ?

(1/2) x 24 x d₂ = 84

12 x d₂ = 84

d₂ = 84 / 12

= 7 cm

So, the length of the other diagonal is 7 cm.

Example 5 :

The diagonal of a quadrilateral are perpendicular bisectors of each other. If the length of one diagonal is 3 cm and the area of the quadrilateral is 180 cm², find the length of the other diagonal.

Solution :

Every quadrilateral will have four sides. In rhombus, the diagonals will bisect each other.

Area of rhombus = 180 cm²

d₁ = 3 cm

(1/2) x d₁ x d₂ = 180

(1/2) x 3 x d₂ = 180

1.5 x d₂ = 180

d₂ = 180 / 1.5

d₂ = 120

So, the length of the other diagonal is 120 cm.

Example 6 :

The length of one of the diagonals of a kite is 4 cm longer than twice the length of the other diagonal. The area of the kite is 15 cm². Find the length of each diagonal.

Solution :

Let x be the length of the other diagonal. 

Length of one diagonal = 2x + 4

Area of kite = 15

(1/2) x (2x + 4) = 15

2x² + 4x = 30

2x² + 4x - 30 = 0

Dividing by 2, we get

x² + 2x - 15 = 0

(x + 5)(x - 3) = 0

x = -5 and x = 3

Length of one diagonal = 3 cm

Length of other diagonal = 2(3) + 4

= 10 cm

Example 7 :

The length of one of the diagonals of a rhombus is 5 cm less than the length of the other diagonal. The area of the rhombus is 33 cm². Find the length of each diagonal.

Solution :

Let x be the length other diagonal.

Length of one diagonal = x - 5

Area of rhombus = 33

(1/2) x (x - 5) = 33

x² - 5x = 66

x² - 5x - 66 = 0

(x - 11) (x + 6) = 0

x = 11 and x = -6

x - 5 ==> 11 - 5 ==> 6 cm

So, length of each diagonals are 11 cm and 6 cm respectively.

Example 8 :

Show that the points A(2, –1), B(3, 4), C(–2, 3) and D(–3, –2) forms a rhombus but not a square. Find the area of the rhombus also.

Solution :

By proving the diagonals are bisecting each other at right angle, we can prove that the shape is rhombus not a square.

Slope AC x Slope of BD = -1

-1(1) = -1

-1 = -1

Since the diagonals are perpendicular it must be a square.

Length of diagonal AC = √[(x₂ - x₁)² + (y₂ - y₁)²]

= √[(-2-2)² + (3+1)²]

= √[(-4)² + 4²]

= √(16+16)

= √32

Length of diagonal BD = √[(-3-3)² + (-2-4)²]

= √[(-6)² + (-6)²]

= √(36+36)

= √72

Area of rhombus = (1/2) √32 √72

= (1/2) x 4√2 (6√2)

= 12(2)

= 24 square units.

So, the required area is 24 square units.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.