HOW TO FIND THE ANGLE BETWEEN TWO VECTORS

How to Find the Angle Between Two Vectors :

Here we are going to see how to find the angle between two vectors.

If θ is the angle between the vectors and a vector and b vector, then

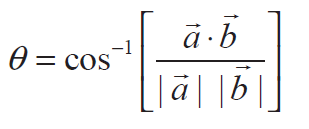
Let us look into some example problems to understand finding angle between two vectors.

Question 1 :

If a vector and b vector are two vectors such that |a| = 10,|b| = 15 and a . b = 75√2, find the angle between a and b.

Solution :

θ  =  cos^-1[75√2/(10)(15)]

θ  =   cos^-1(√2/2)

θ  =   cos^-1(1/√2)

θ  =  π/4

Question 2 :

Find the angle between the vectors

(i) 2i vector + 3j vector − 6k vector and 6i vector − 3j vector + 2k vector

Solution :

Let a vector  =  2i vector + 3j vector − 6k vector and 

b vector  =  6i vector − 3j vector + 2k vector

Angle between two vector :

θ  =  cos^-1 [a vector . b vector/ |a| |b|]

a vector . b vector  =  2(6) + 3(-3) + (-6)(2)

  =  12 - 9 - 12

  =  -9

|a vector|  =  |2i vector + 3j vector − 6k vector|

r  =  √(2² + 3² + (-6)²)  =  √(4 + 9 + 36)

  =  √49  =  7

|b vector|  =  |6i vector - 3j vector + 2k vector|

r  =  √(6² + (-3)² + 2²)  =  √(36 + 9 + 4)

  =  √49  =  7

θ  =  cos^-1 [-9/(7)(7)]

θ  =  cos^-1 [-9/49]

(ii) i vector − j vector and j vector − k vector.

Let a vector  =  i vector − j vector and 

b vector  =  j vector − k vector

Solution :

Angle between two vector :

θ  =  cos^-1 [a vector . b vector/ |a| |b|]

a vector . b vector  =  1(0) + (-1)1 + 0(-1) 

  =  0 - 1 + 0

  =  -1

|a vector|  =  |i vector - j vector|

r  =  √(1² + (-1)²)  =  √(1 + 1)  =  √2

|b vector|  =  |j vector - k vector|

r  =  √(1² + (-1)²)  =  √(1+1)  =  √2

θ  =  cos^-1 [-1/( √2)( √2)]

θ  =  cos^-1 [-1/2]

θ  =  2π/3

Question 3 :

If a vector, b vector, c vector are three vectors such that a vector + 2b vector + c vector = 0 vector and |a|= 3, |b| = 4, |c| = 7,  find the angle between a vector and b vector.

Solution :

a vector + 2b vector + c vector = 0 vector

|a + 2b| vector =  |-c| vector

|a + 2b|² =  |-c|²

|a|² + |2b|² + 2|a||2b|  =  |c|²

|a|² + 4|b|² + 4|a vector| |b vector |  =  |c|²

|a|² + 4|b|² + 4(a. b)  =  |c|²

|a|² + 4|b|² + 4 |a| |b| cos θ  =  |c|²

3² + 4(4)² + 4 (3)(4) cos θ  =  7²

9 + 64 + 48 cos θ  =  49

73 + 48 cos θ  =  49

48 cos θ  =  49 - 73

48 cos θ  =  -24

θ  =  cos^-1 (-24/48)

θ  =  cos^-1 (-1/2)

θ  =  2π/3

After having gone through the stuff given above, we hope that the students would have understood,"How to Find the Angle Between Two Vectors"

Apart from the stuff given in "How to Find the Angle Between Two Vectors",  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.