HOW TO FIND nth TERM OF ARITHMETIC SEQUENCE

Examples 1-4 : Find the nth term of the following arithmetic sequences :

Example 1 :

4, 9, 14, …………

Solution :

Common difference :

d = a₂ – a₁

= 9 – 4

= 5

n^th term of an arithmetic sequence :

a_n = a₁ + (n - 1)d

Substitute a₁ = 4 and d = 5.

a_n = 4 + (n - 1)(5)

= 4 + 5n - 5

= 5n - 1

Example 2 :

125, 120, 115, 110, …………

Solution :

Common difference :

d = a₂ – a₁

= 120 – 125

= -5

n^th term of an arithmetic sequence :

a_n = a₁ + (n - 1)d

Substitute a₁ = 125 and d = -5.

a_n = 125 + (n - 1)(-5)

= 125 - 5n + 5

= 130 - 5n

Example 3 :

24, 23¼, 22½, 21¾, …………

Solution :

Common difference :

d = a₂ – a₁

= 23¼ - 24

= 93/4 - 24

= (93 - 96)/4

= -3/4

n^th term of an arithmetic sequence :

a_n = a₁ + (n - 1)d

Substitute a₁ = 24 and d = -3/4.

a_n = 24 + (n - 1)(-3/4)

= 24 - 3n/4 + 3/4

= 24 + 3/4 - 3n/4

= (96 + 3)/4 - 3n/4

= 99/4 - 3n/4

Example 4 :

√2, 3√2, 5√2, …………

Solution :

Common difference :

d = a₂ – a₁

= 3√2 - √2

= 2√2

n^th term of an arithmetic sequence :

a_n = a₁ + (n - 1)d

Substitute a₁ = √2 and d = 2√2.

a_n = √2 + (n - 1)(2√2)

= √2 + (2√2)n - 2√2

= (2√2)n - √2

Example 5 :

The 10^th and 18^th terms of an arithmetic sequence are 41 and 73 respectively. Find the n^th term.

Solution :

(2) - (1) :

8d = 32

d = 4

Substitute d = 4 in (1).

a₁ + 9(4) = 41

a₁ + 36 = 41

a₁ = 5

n^th term of an arithmetic sequence :

a_n = a₁ + (n - 1)d

Substitute a₁ = 5 and d = 4.

a_n = 5 + (n - 1)(4)

= 5 + 4n - 4

= 4n + 1

Example 6 :

Find n so that the n^th terms of the following two arithmetic sequences are the same.

1, 7, 13, 19, …………

100, 95, 90, …………

Solution :

Part (i) :

1, 7, 13, 19, …………

Common difference :

d = a₂ – a₁

= 7 - 1

= 6

n^th term of an arithmetic sequence :

a_n = a₁ + (n - 1)d

Substitute a₁ = 1 and d = 6.

a_n = 1 + (n - 1)(6)

= 1 + 6n - 6

= 6n - 5

Part (ii) :

100, 95, 90, …………

Common difference :

d = a₂ – a₁

= 95 - 100

= -5

n^th term of an arithmetic sequence :

a_n = a₁ + (n - 1)d

Substitute a₁ = 100 and d = -5.

a_n = 100 + (n - 1)(-5)

= 100 - 5n + 5

= 105 - 5n

Solve for n :

Given : n^th terms of the two arithmetic sequences are the same.

6n - 5 = 105 - 5n

11n - 5 = 105

11n = 110

n = 10

Example 7 :

Online bidding for a purse increases by $5 for each bid after the $60 initial bid

a. Write a function that represents the arithmetic sequence.

b. Graph the function.

c. The winning bid is $105. How many bids were there?

Solution :

a) f(n) = a + (n - 1) d

a = 60, d = 65 - 60 ==> 5

f(n) = 60 + (n - 1)5

= 60 + 5n - 5

= 5n + 55

b) (1, 60) (2, 65) (3, 70) and (4, 75)

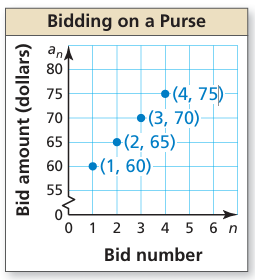
c)  When number of bids = 105

f(n) = 5n + 55

105 = 5n + 55

105 - 55 = 5n

5n = 50

n = 50/5

n = 10

There were 10 bids.

Example 7 :

A carnival charges $2 for each game after you pay a $5 entry fee.

a. Write a function that represents the arithmetic sequence.

b. Graph the function.

c. How many games can you play when you take $29 to the carnival?

Solution :

a)  f(n) = a + (n - 1) d

a = 7, d = 9 - 7 ==> 2

f(n) = 7 + (n - 1)2

= 7 + 2n - 2

f(n) = 2n + 5

b) (1, 7) (2, 9) (3, 11) and (4, 13)

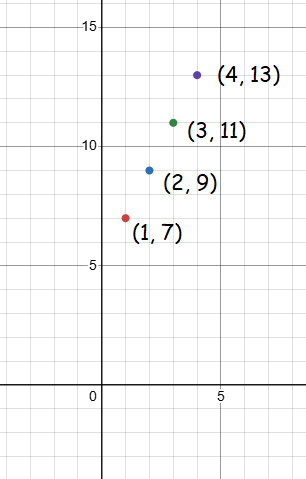
c)  f(n) = 2n + 5

Amount taken = 29

29 = 2n + 5

29 - 5 = 2n

2n = 24

n = 24/2

n = 12

So, the required number of games is 12.

Example 8 :

Firewood is stacked in a pile. The bottom row has 20 logs, and the top row has 14 logs. Each row has one more log than the row above it. How many rows of logs are in the pile?

Solution :

Number of logs in the first row = 20

Number of logs in the last row = 14

When we look from the bottom to top, each row will have 1 less log.

f(n) = a + (n - 1)d

14 = 20 + (n - 1) (-1)

14 - 20 = -n + 1

-6 = -n + 1

n = 1 + 6

n = 7

So, there are 7 rows of logs.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.