HOW TO FIND NATURE OF SOLUTION OF QUADRATIC EQUATION WITH GRAPH

To obtain the roots of the quadratic equation in the form ax² + bx + c = 0 graphically, first we have to  draw the graph of y = ax² + bx + c .

The solutions of the quadratic equation are the x coordinates of the points of intersection of the curve with X axis.

Finding the Nature of Solutions of Quadratic Equations Graphically

Solved Questions

Question 1 :

Graph the following quadratic equations and state their nature of solutions.

x² − 9x + 20  =  0

Solution :

Draw the graph for the function y = x² − 9x + 20

Let us give some random values of x and find the values of y.

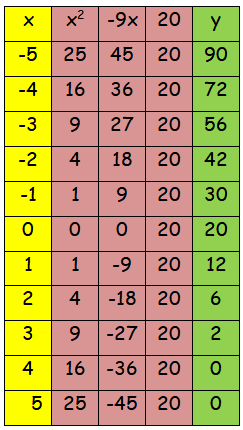
To find the x-coordinate of the vertex of the parabola, we may use the formula x = -b/2a

x = -(-9)/2(1)  =  9/2

By applying x = 9/2, we get the value of y.

y = (9/2)² - 9(9/2) + 20

y = (81/4) - (81/2) + 20

y = (81 - 162 + 80)/4  =  -1/4

Vertex (9/2, - 1/4)

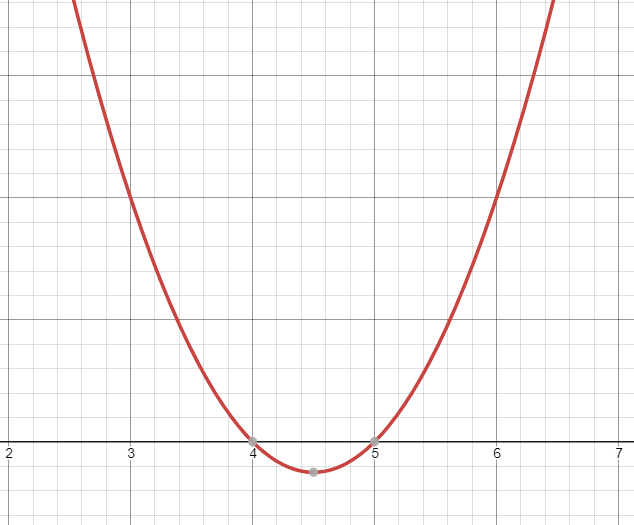
The graph of the given parabola intersects the x-axis at two distinct points. Hence it has real and unequal roots.

Question 2 :

Graph the following quadratic equations and state their nature of solutions.

x² − 4x + 4 = 0

Solution :

Let us give some random values of x and find the values of y.

Points to be plotted :

(-4, 36) (-3, 25) (-2, 16) (-1, 9) (0, 4) (1, 1) (2, 0) (3, 1) (4, 4)

To find the x-coordinate of the vertex of the parabola, we may use the formula x = -b/2a

x = -(-4)/2(1)  =  4/2  =  2

By applying x = 2, we get the value of y.

y = 2² - 4(2) + 4

y = 4 - 8 + 4

y = 0

Vertex (2, 0)

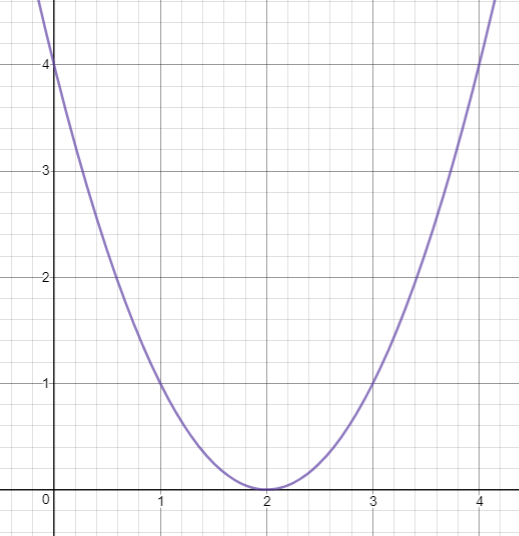
The graph of the given parabola intersects the x-axis at only one point. it has real and equal roots.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.