HOW TO FIND MISSING COORDINATES USING DISTANCE FORMULA

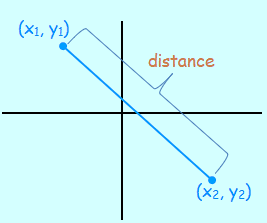
Using two endpoints of the line segment, we can find distance between two points.

D  =  √[(x₂ – x₁)² + (y₂ – y₁)²]

Here D is the distance and the coordinates of two points are (x₁, y₁) and (x₂, y₂)

Find a given that :

Example 1  :

P(2, 3) and Q(a, -1) are 4 units apart

Solution  :

Given points, P(2, 3) and Q(a, -1)

P(2, 3) ----->(x₁, y₁)

Q(a, -1) ----->(x₂, y₂)

Using distance Formula :

Here, d  =  4 units.

d  =  √[(x₂ – x₁)² + (y₂ – y₁)²]

4  =  √[(a – 2)² + (-1 – 3)²]

4  =  √[(a – 2)² + (-4)²]

4  = √[(a – 2)² + 16]

4  =  √[(a² – 4a + 4) + 16]

4  =  √(a² – 4a + 20)

Taking square root on both sides, we get

(4)²  =  [√(a² – 4a + 20)]²

16  =  a² – 4a + 20

a² – 4a + 20 – 16  =  0

a² - 4a + 4  =  0

By factorization, we get

(a – 2) (a – 2)  =  0

a  =  2

So, the value of a is 2

Example 2 :

P(-1, 1) and Q(a, -2) are 5 units apart

Solution :

Given points, P(-1, 1) and Q(a, -2)

P(-1, 1) ----->(x₁, y₁)

Q(a, -2) ----->(x₂, y₂)

Using distance Formula :

Here, d  =  5 units.

d  =  √[(x₂ – x₁)² + (y₂ – y₁)²]

5  =  √[(a – (-1))² + (-2 – 1)²]

5  =  √[(a + 1)² + (-3)²]

5  = √[(a + 1)² + 9]

5  =  √[(a² + 2a + 1) + 9]

5  =  √(a² + 2a + 10)

Taking square root on both sides, we get

(5)²  =  [√(a² + 2a + 10)]²

25  =  a² + 2a + 10

a² + 2a + 10 – 25  =  0

a² + 2a - 15  =  0

By factorization, we get

(a – 3) (a + 5)  =  0

a  =  3 or -5

So, the value of a is 3 or -5

Example 3 :

X(a, a) is √8 units from the origin.

Solution :

Given points, X(a, a) and the origin O(0, 0)

X(a, a) ----->(x₁, y₁)

O(0, 0) ----->(x₂, y₂)

Using distance Formula :

Here, d  =  √8 units.

d  =  √[(x₂ – x₁)² + (y₂ – y₁)²]

√8  =  √[(0 – a)² + (0 – a)²]

√8  =  √[(-a)² + (-a)²]

√8  =  √(a² + a²)

√8  = √(2a²)

Taking square root on both sides, we get

(√8)²  = [√(2a²)]²

8  =  2a²

4  =  a²

a  =  ±2

So, the value of a is ±2

Example 4 :

A(0, a) is equidistant from P(3, -3) and Q(-2, 2)

Solution :

Let the point on y-axis be A(0, a)

Now, A(0, a) is equidistant from the points P(3, -3) and Q(-2, 2)

AP  =  AQ

Using distance Formula :

Distance between A(0, a) and P(3, -3)

A(0, a) ----->(x₁, y₁)

P(3, -3) ----->(x₂, y₂)

=  √[(x₂ – x₁)² + (y₂ – y₁)²]

=  √[(3 – 0)² + (-3 – a)²]

=  √[(3)² + (-3 – a)²] 

=  √[9 + (-3 – a)²] -------(1)

Distance between A(0, a) and Q(-2, 2)

A(0, a) ----->(x₁, y₁)

P(-2, 2) ----->(x₂, y₂)

=  √[(x₂ – x₁)² + (y₂ – y₁)²]

=  √[(-2 – 0)² + (2 – a)²]

=  √[(-2)² + (2 – a)²] 

=  √[4 + (2 – a)²] -------(2)

Equating (1) and (2), we get

√[9 + (-3 – a)²]  =  √[4 + (2 – a)²]

Taking square root on both sides, we get

(√[9 + (-3 – a)²])²  =  (√[4 + (2 – a)²])²

9 + (-3 – a)²  =  4 + (2 – a)²

9 + 9 + 6a + a²  =  4 + 4 – 4a + a²

18 + 6a + a²  =  8 – 4a + a²

18 + 6a + a² - 8 + 4a - a²  =  0

10a + 10  =  0

10a  =  -10

a  =  -1

So, the value of a is -1

Example 5 :

If the coordinates one point on the circle is (-2, 3) and its radius is 3 unit the coordinates of its center are (a , 3), then a = ______

Solution :

Radius of the circle = distance between center and one of the point on the circle

 √[(x₂ – x₁)² + (y₂ – y₁)²] = 3

 √[(a + 2)² + (3 - 3)²] = 3

 √(a + 2)² = 3

a + 2 = 3

a = 3 - 2

a = 1

Example 6 :

If P (–1, 1) is the midpoint of the line segment joining A(–3, b) and B (1, b+4 ) then b = ____ ?

(a) 1            (b) –1               (c) 2     (d) 0

Solution :

Distance between the points AP and BP are equal.

=  √[(x₂ – x₁)² + (y₂ – y₁)²]

A(–3, b) and P (–1, 1)

=  √[(-1 + 3)² + (1 - b)²]

=  √[2² + (1 - b)²]

=  √4 + (1 - b)² ----(1)

B (1, b+4 ) and P (–1, 1)

=  √[(1 + 1)² + (b + 4 - 1)²]

=  √[(2)² + (b + 3)²]

=  √4 + (b + 3)²] ------(2)

(1) = (2)

√4 + (1 - b)²=  √4 + (b + 3)²]

1 - b = b + 3

-b - b = 3 - 1

-2b = 2

b = -1

So, the value of b is -1.

Example 7 :

If the point P (k-1 ,2) is equidistant from the points A (3, k) and B( k, 5) find the values of k.

Solution :

√(3 - (k - 1))² +  (k - 2)²=  √(k - (k - 1))² + (5 - 2)²]

√(3 - k + 1)² +  (k - 2)²=  √(k - k + 1)² + 3²]

√(4 - k )² +  (k - 2)²=  √10

(4 - k )² +  (k - 2)² =  10

16 - 8k + k² + k² -4k + 4 = 10

2k² - 12k + 20 = 10

2k² - 12k + 10 = 0

k² - 6k + 5 = 0

(k - 1)(k - 5) = 0

k = 1 and k = 5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.