HOW TO FIND MAXIMUM AND MINIMUM VALUE OF A FUNCTION

The following steps would be useful to find the maximum and minimum value of a function using first and second derivatives. 

Example 1 :

Determine the maximum value of the function :

f(x) = 4x - x² + 3

Solution :

Find the first derivative of f(x). 

f'(x) = 4(1) - 2x + 0

= 4 - 2x

Equate the first derivative to zero, that is f'(x) = 0.

4 - 2x = 0

2(2 - x) = 0

2 - x = 0

x = 2

Find the second derivative of f(x).

f'(x) = 4 - 2x

f"(x) = 0 - 2(1)

f"(x) = -2

Substitute the critical number x = 2 in f"(x).

f"(2) = -2 < 0

So, f(x) is maximum at x = 2.

To find the maximum value, substitute x = 2 in f(x).

f(2) = 4(2) - 2² + 3

= 8 - 4 + 3

= 11 - 4

= 7

Therefore the maximum value of the function f(x) is 7.

Justification :

We can justify our answer by graphing the function f(x).

f(x) = 4x - x² + 3

The given function is the equation of parabola. Replace f(x) by y. 

y = -x² + 4 x + 3

Write the above equation of parabola in vertex form.

y = -(x² - 4 x - 3)

y = -[x² - 2(x)(2) + 2² - 2² - 3]

y = -[(x - 2)² - 4 - 3]

y = -[(x - 2)² - 7]

y = -(x - 2)² + 7

The above equation is in the form y = a(x - h)² + k.

a = -1

Vertex (h, k) = (2, 7)

Because 'a' is negative the parabola opens down. So, we have only the maximum value for y, that is the y-coordinate at the vertex, which is 7.

The answer is justified.

Example 2 :

Determine the maximum and minimum values of the function :

f(x) = 2x³ + 3x² - 36x + 1

Solution :

Find the first derivative of f(x). 

f'(x) = 2(3x²) + 3(2x) - 36(1) + 0

= 6x² + 6x - 36

Equate the first derivative to zero, that is f'(x) = 0.

6x² + 6x - 36 = 0

Divide both sides by 6.

x² + x - 6 = 0

Factor and solve. 

(x - 2)(x + 3) = 0

Find the second derivative of f(x).

f'(x) = 6x² + 6x - 36

f"(x) = 6(2x) + 6(1) - 0

f"(x) = 12x + 6

Substitute the critical numbers x = 2 and x = -3 in f"(x).

When x = 2, f"(x) > 0, the function f(x) is minimum at

x = 2 

When x = -3, f"(x) > 0, the function f(x) is maximum at

x = -3

To find the maximum and minimum values of the given function, substitute x = -3 and x = 2 in f(x).

Maximum value : 

f(-3) = 2(-3)³ + 3(-3)² - 36(-3) + 1

= 2(-27) + 3(9) + 108 + 1

= -54 + 27 + 108 + 1

= 82

Minimum value : 

f(2) = 2(2)³ + 3(2)² - 36(2) + 1

= 2(8) + 3(4) - 72 + 1

= 16 + 12 - 72 + 1

= -43

Example 3 :

Mona has 400 yards of fencing to enclose a rectangular area. Find the dimensions of the rectangle that maximize the enclosed area. What is the maximum area?

Solution :

Let 𝓵 and w be the length and width of the rectangle respectively.

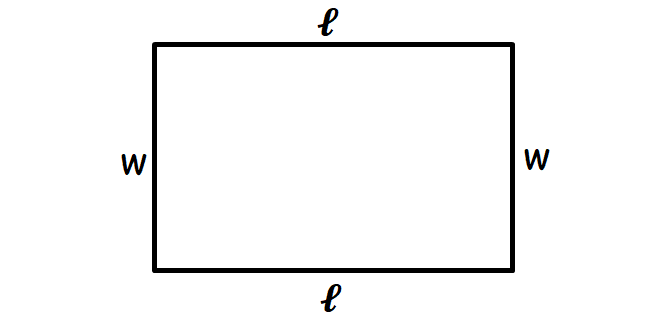
Total length of fence = 400 yards

2𝓵 + 2w = 400

Divide both sides by 2.

𝓵 + w = 200

Subtract w from both sides.

𝓵 = 200 - w ----(1)

Area of a rectangle = 𝓵 ⋅ w

= (200 - w) ⋅ w

= 200w - w²

Let A(w) be the area of the rectangle.

A(w) = = 200w - w² ----(2)

Find the first derivative of A(w). 

A'(w) = 200 - 2w

Equate the first derivative to zero and solve for w, which is called critical number.

200 - 2w = 0

-2w = -200

w = 100

Find the second derivative of A(w).

A'(w) = 200 - 2w

A"(w) = -2

Substitute the critical number w = 100 in A"(w).

A"(100) = -2 < 0

So, A(w) is maximum at w = 100.

Substitute w = 100 into (1).

𝓵 = 200 - 100

𝓵 = 100

The area is maximum when

length = 100 yards

width = 100 yards

To find the maximum area, substitute w = 100 into (2).

A(100) = 200(100) - 100²

= 20000 - 10000

= 10000

Therefore, the maximum area is 10000 square yards.

Example 4 :

The sum of two numbers is 10. Find the smallest possible value for the sum of their squares.

Solution :

Let x and y be the two numbers.

x + y = 10

y = 10 - x ----(1)

Sum of their squares :

= x² + y²

= x² + (10 - x)²

= x² + 10² - 2(10)(x) + x²

= x² + 100 - 20x + x²

= 2x² - 20x + 100

Let S(x) be the sum of the their squares.

S(x) = 2x² - 20x + 100

Find the first derivative of P(x).

S'(x) = 4x - 20

Find the second derivative of P(x).

S"(x) = 4

Equate the first derivative to zero and solve for x, which is called critical number.

S'(x) = 0

4x - 20 = 0

4x = 20

x = 5

Substitute x = 5 into S"(x) = 4.

S"(5) = 4

S"(5) = 4 > 0

So, S(x) is minimum at x = 4.

Subsitute x = 5 into (1).

y = 10 - 5

y = 5

When the two numbers are 5 and 5, the sum of their squares is minimum.

The smallest possible value for the sum of their squares :

= 5² + 5²

= 25 + 25

= 50

Example 5 :

The total cost of a firm is

where C(x) is the total cost and x is output. A tax at a rate of $2 per unit of output is imposed and the producer adds it to his cost. If the market demand function is given by

p = 2530 - 5x

where p is the price per unit of output in dollars, find the profit maximising output and price for maximum profit. 

Solution :

Since a tax of $2 per unit of output is imposed, the total tax for x units of output is 2x. The producer adds this tax to his cost.

Then, the total new cost is

Let R(x) be the revenue for the ouput of x units.

Revenue : Price x Output

R(x) = (2530 - 5x)x

R(x) = 2530x - 5x²

Let P(x) be the profit for the ouput of x units.

Profit = Revenue - Total Cost

P(x) = R(x) - C(x)

Find the first derivative of P(x).

P'(x) = -x² + 2500

Find the second derivative of P(x).

P"(x) = -2x

Equate the first derivative to zero and solve for x, which is called critical number.

P'(x) = 0

-x² + 2500 = 0

-x² = -2500

x² = 2500

x = ± 50

x = -50  or  50

Output can never be a negative value.

So, x = 50.

Substitute x = 50 into P"(x) = -2x.

P"(50) = -2(50)

P"(50) = -100 < 0

So, P(x) is maximum at x = 50.

Therefore, profit maximising output is 50 units.

Subsitute x = 50 into demand function p = 2530 - 5x.

p = 2530 - 5(50)

p = 2530 - 250

p = 2280

Therefore, the price for maximum profit is $2280.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.