HOW TO FIND LIMITS BY LOOKING AT A GRAPH

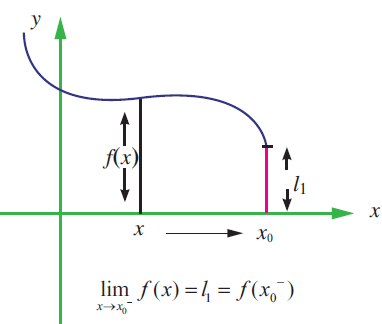
Left hand limit

We say that the left-hand limit of f(x) as x approaches x₀ (or the limit of f(x) as x approaches from the left) is equal to l₁ if we can make the values of f(x) arbitrarily close to l₁ by taking x to be sufficiently close to x₀ and less than x₀. It is symbolically written as 

f(x₀^-)  =  lim x ->x₀^- f(x)  =  l₁

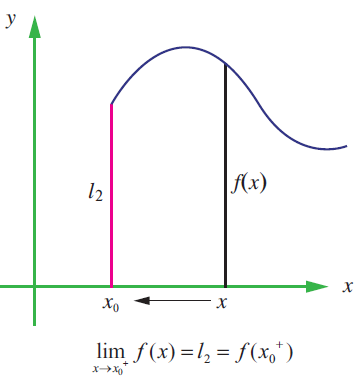
Right hand limit

We say that the right-hand limit of f(x) as x approaches x₀ (or the limit of f(x) as x approaches from the right) is equal to l₂ if we can make the values of f(x) arbitrarily close to l₂ by taking x to be sufficiently close to x₀ and greater than x₀. It is symbolically written as 

f(x₀⁺)  =  lim x ->x₀⁺ f(x)  =  l₂

From the above discussions we conclude that

lim x->x₀ f(x)  =  L exists if the following hold :

(i) lim x->x₀+ f(x) exists, 

(ii)  lim x->x₀- f(x) exists, and

(iii)  lim x->x₀+ f(x)  =   lim x->x₀- f(x)  =  L

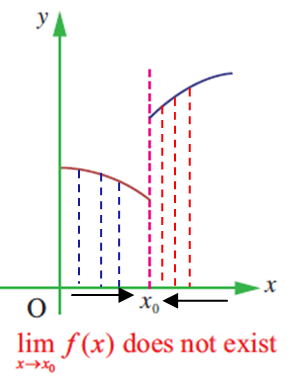
When we get different values for f(x) as x₀ approaches from left and from right, we may say that the function does not exist.

The picture given below will illustrate the concept.

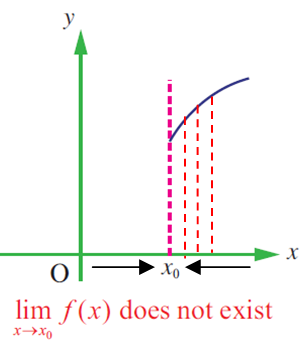
There is no function to the left of x₀. Hence the function is not defined.

Example 1 :

Use the graph to find the limits (if it exists). If the limit does not exist, explain why?

lim _x->3 (4 - x)

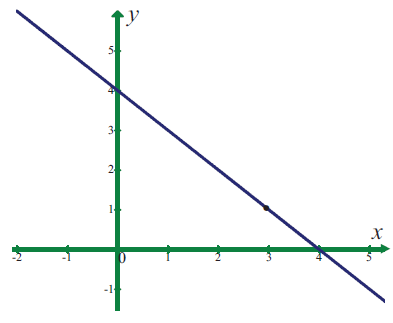
Solution :

lim _x->3 f(x)  =  4 - 3  =  1

lim _x->3- f(x)  =  lim _x->3+ f(x)  =  lim _x->3 f(x)

The function is defined at x -> 3. Hence the required limit is 1.

Example 2 :

Use the graph to find the limits (if it exists). If the limit does not exist, explain why?

lim _x->1 (x² + 2)

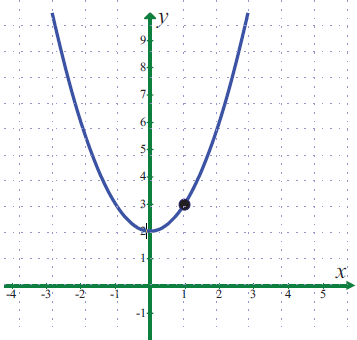
Solution :

lim _x->1 f(x)  =  x² + 2  =  1² + 2  =  3

lim _x->1^- f(x)  =  lim _x->1+ f(x)  =  lim _x->1 f(x)

The function is defined at x -> 1. Hence the required limit is 3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.