HOW TO FIND LENGTH OF LATUS RECTUM OF PARABOLA

Consider the graph of a parabola shown below.

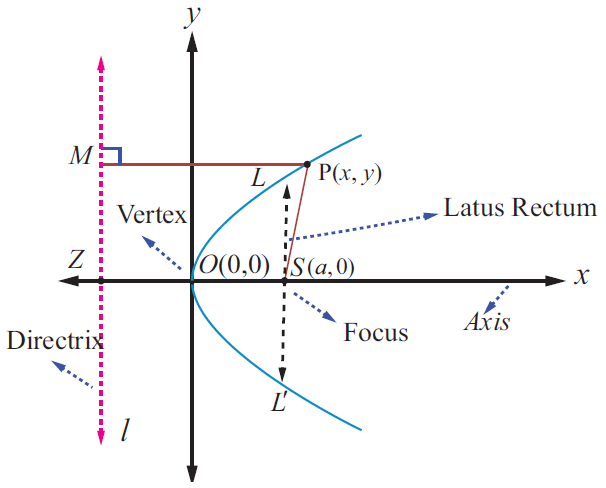
The parabola opens to the right with vertex (0, 0).

The equation of the parabola shown above in standard form :

y² = 4ax

Latus rectum LL' passes through the focus (a, 0).

Hence the point L is (a, y₁).

There fore,

y₁² = 4a(a)

y₁² = 4a²

Take square root on both sides.

y₁ = ±√(4a²)

y₁ = ±2a

y₁ = 2a or -2a

The end points of latus rectum are (a, 2a) and (a,-2a).

Therefore length of the latus rectum LL' = 4a.

Find the length of latus rectum of the following parabolas :

Example 1 :

x² = -4y

Solution :

The given equation equation of the parabola in standard form.

Comparing x² = -4y and x² = -4ay,

4a = 4

So, the length of latus rectum is 4 units.

Example 2 :

y² - 8x + 6y + 9 = 0

Solution :

The given equation of the parabola is not in standard form.

Write the equation of the parabola in standard form. 

y² - 8x + 6y + 9 = 0

y² + 6y = 8x - 93

y² + 2(y)(3) = 8x - 9

y² + 2(y)(3) + 3² - 3² = 8x - 9

(y + 3)² - 3² = 8x - 9

(y + 3)² - 9 = 8x - 9

(y + 3)² = 8x

(y + 3)² = 8(x - 0)

Now, the equation of the parabola is in standard form.

Comparing (y - k)² = 4a(x - h) and (y + 3)² = 8(x - 0),

4a = 8

So, the length of latus rectum is 8 units.

Example 3 :

x² - 2x + 16y + 17 = 0

Solution :

The given equation of the parabola is not in standard form.

Write the equation of the parabola in standard form. 

x² - 2x = -16y - 17

x² - 2(x)(1) = -16y - 17

x² - 2(x)(1) + 1² - 1² = -16y - 17

(x - 1)² - 1² = -16y - 17

(x - 1)² - 1 = -16y - 17

(x - 1)² = -16y - 16

(x - 1)² = -16(y + 1)

Now, the equation of the parabola is in standard form.

Comparing (x - h)² = -4a(y - k) and (x - 1)² = -16(y + 1),

4a = 16

So, the length of latus rectum is 16 units.

Example 4 :

y = 2x²+ 3x + 4

Solution :

The given equation of the parabola is not in standard form.

Write the equation of the parabola in standard form. 

y = 2x²+ 3x + 4

or

2x²+ 3x = y - 4

4a = 1/2 or 0.5

So, the length of latus rectum is 0.5 units.

Example 5 :

Find the equation of the parabola with endpoints of the latus rectum at (-1, 4) and (5, 4).

Solution :

Midpoint of the latus rectum = focus

Midpoint = (x₁ + x₂)/2, (y₁ + y₂)/2

= (-1 + 5)/2, (4 + 4)/2

= 4/2, 8/2

= (2, 4)

By observing the endpoints of the latus rectum, the parabola is symmetric about x-axis. The parabola opens vertically.

By joining the endpoints of the latus rectum, the parabola must opens up or down.

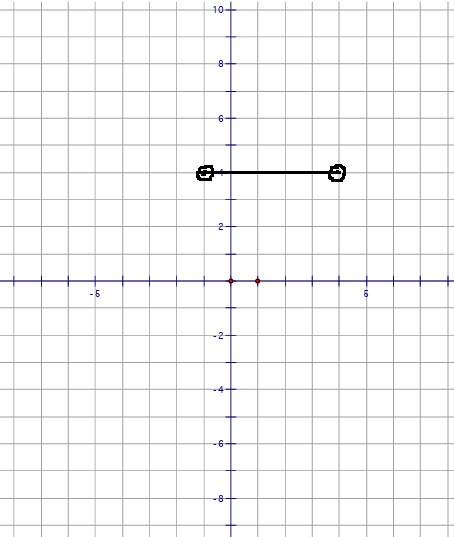
Length of latus rectum = 4a

= √(x₂ - x₁)² + (y₂ - y₁)²

= √(5 - (-1))² + (4 - 4)²

= √(5 + 1)² + 0

= √6²

= +6 or -6

4a = -6 and 4a = -6

a = 6/4

= 3/2 and -3/2

(x - h)² = 4a(y - k)

Vertex (h, k - a) ==> (2, 4 - (3/2))

= (2, 5/2)

Vertex (h, k - a) ==> (2, 4 - (-3/2))

= (2, 11/2)

(x - h)² = 4a(y - k)

(x - 2)² = 4(3/2)(y + 5/2)

(x - 2)² = 6(y + 5/2)

(x - 2)² = 3(2y + 5)

x² - 4x + 4 = 6y + 15

x² - 4x - 6y + 4 - 15 = 0

x² - 4x - 6y - 11 = 0

(x - h)² = 4a(y - k)

(x - 2)² = 4(-3/2)(y + 11/2)

(x - 2)² = -6(2y + 11)/2

(x - 2)² = -3(2y + 11)

x² - 4x + 4 = -6y - 33

x² - 4x + 6y + 4 + 33 = 0

x² - 4x + 6y + 37 = 0

Rewrite the equation to match the standard form. Find the coordinates of the focus, and the equation of the directrix. Find the length of the latus rectum. Graph.

2y + x² + 8x + 18 = 0

The given equation of the parabola is not in standard form.

Write the equation of the parabola in standard form. 

2y + x² + 8x + 18 = 0

x² + 8x = -2y - 18

x² + 2x (4) + 4² - 4² = -2y - 18

(x + 4)² - 4² = -2y - 18

(x + 4)² - 16 = -2y - 18

(x + 4)² = -2y - 18 + 16

(x + 4)² = -2y - 2

(x + 4)² = -2(y + 1)

The parabola is symmetric about y-axis and it opens downward.

(x + 4)² = -2(y + 1)

Comparing with,

(x - h)² = 4a(y - k)

Vertex : (h, k) ==> (-4, -1)

Focus (-4, -1 - 1/2) ==> (-4, -3/2)

4a = 2

So, the length of latus rectum is 2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.