HOW TO FIND LCM FROM TWO POLYNOMIALS AND GCD

Practice Problems

Problem 1 :

Find the LCM of the following polynomials whose GCD is (a - 2).

(a² + 4a −12)  and  (a² −5a + 6)

Solution :

Let f(x)  =  a² + 4a −12, g(x)  =  a² −5a + 6.

GCD is (a -2)

f (x) × g(x) = LCM × GCD

LCM  =  [f(x) × g(x)] / GCD

LCM  =  [(a + 6)(a - 2)  (a - 3)(a - 2)] /  a -2

LCM  =  (a + 6)(a - 2)  (a - 3)

Problem 2 :

Find the LCM of the following polynomials whose GCD is (x - 3a).

(x ⁴ -27a³x)  and  (x -3a)²

Solution :

Let f(x)  =  x ⁴ -27a³x, g(x)  =   (x -3a)²

GCD is (x -3a)

f (x) × g(x) = LCM × GCD

LCM  =  [f(x) × g(x)] / GCD

LCM  =  [x(x- 3a)(x²-3ax+9a²)(x -3a)²] /  (x -3a)

LCM  =  x(x²-3ax+9a²)(x -3a)²

How to Find GCD from Two Polynomials and LCM

Problem 1 :

Find the GCD of the following polynomials.  

12(x⁴ -x³)  and  8(x⁴ −3x³ +2x²)

Given that LCM is 24x³(x -1)(x -2).

Solution :

Let f(x)  =  12(x⁴ -x³), g(x)  =  8(x⁴ −3x³ +2x²)

LCM  =  24x³(x -1)(x-2)

GCD  =  24x³(x -1)(x -2)

f (x) × g(x) = LCM × GCD

GCD  =  [f(x) × g(x)] / LCM

GCD  =  [12x³(x - 1) 8x²(x² - 3x + 2)]/ 24x³(x -1)(x -2)

GCD  =  4x²(x-1)

Problem 2 :

Find the GCD of the following polynomials.  

(x³ + y³)  and  (x⁴ + x²y² + y⁴)

Given that LCM is (x³ + y³)(x² + xy + y²).

Solution :

Let f(x)  =  (x³ + y³), g(x)  =  (x⁴ + x²y² + y⁴)

LCM is (x³ + y³)(x² + xy + y²)

LCM  =  (x³ + y³)(x² + xy + y²)

f (x) × g(x) = LCM × GCD

GCD  =  [f(x) × g(x)] / LCM

GCD  =  [ (x³ + y³)(x²-xy+ y² )(x²+ xy+ y²)] / (x³ + y³)(x² + xy + y²)

GCD  =  (x² - xy +  y²)

Problem 3 :

LCM and GCD of the two polynomials p(x) and q(x) and the polynomial p(x) are given below. Find q(x). 

LCM  =  a³ −10a² +11a + 70

GCD  =  a - 7

p(x)  =  a² −12a + 35

Solution :

p (x) × q(x)  =  LCM × GCD

Then, 

q(x)  =  (LCM × GCD) / p (x)

=   (a³ −10a² +11a + 70)( a - 7)/(a² −12a + 35)

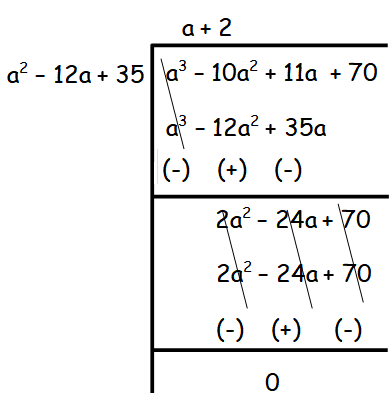
q(x)  =  (a + 2) (a - 7) 

Problem 4 :

LCM and GCD of the two polynomials p(x) and q(x) and the polynomial q(x) are given below. Find p(x). 

LCM = (x² +y²)(x⁴ +x²y²+y⁴)

GCD  =  (x² -y²)(x⁴ −y⁴)

q(x)  =  (x² +y² −xy)

Solution :

p (x) × q(x)  =  LCM × GCD

Then, 

p(x)  =  (LCM × GCD)/q(x)

=  (x² + y²)(x⁴ + x²y² + y⁴)(x² - y²) / (x⁴ − y⁴)(x² + y²− xy)

=  (x⁴ - y⁴)(x⁴ + x²y² + y⁴) / (x⁴ − y⁴)(x² + y²− xy)

=  (x⁴ + x²y² + y⁴) / (x² + y²− xy)

=  [(x² + y²)² - (xy)²] / (x² + y²− xy)

=  (x² - xy + y²)(x² + xy + y²) / (x² − xy + y²)

=  (x²+ xy+ y²)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.