HOW TO FIND HOW MANY WORDS CAN BE FORMED USING ALL THE LETTERS

(i) The vowels and consonants are alternative

Case (i) 

If vowels will occupy odd places, then consonants will occupy even places.

Case (ii) 

If vowels will occupy even places, then consonants will occupy odd places.

Number of ways to fill odd places  =  6!/3!2! 

  =  (6 ⋅ 5 ⋅ 4)/(2 ⋅ 1)

  =  3 ⋅ 5 ⋅ 4  =  60

Number of ways to fill even places  =  6!/2! 

  =  6 ⋅ 5 ⋅ 4 ⋅ 3

  =  360

Number of ways in case (i)  =  60 ⋅ 360  =  21600

Number of ways in case (ii)  =  60 ⋅ 360  =  21600

Total ways  = 21600 + 21600  =  43200

(ii) All the vowels are together

Since all vowels are together, we have to take it as one unit.

Considering the consonants as independent things. So, we have 7 units. Vowels may shuffle them among themselves in 6 places.

So, number of ways  =  (7! ⋅ 6!) / (3!⋅2!⋅2!)

  =  (7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1) ⋅ (6 ⋅ 5)

  =  151200

Hence the total ways is 151200.

(iii) Vowels are never together

To find the answer for the above case, let us follow the step given below.

Vowels are never together

  =  (Number of ways of arranging the letters of the given word without restriction) - (Number of ways of arranging the the letters with vowels together)

  =  [12!/ (3!⋅2!⋅2!)]  - 151200

  =  19958400 - 151200

  =  19807200

(iv) No two vowels are together.

No two vowels are together means, we may fix vowels and consonants in alternate places and any two consonants may be placed between two vowels.

Note : We cannot take more than two consonants at a time.

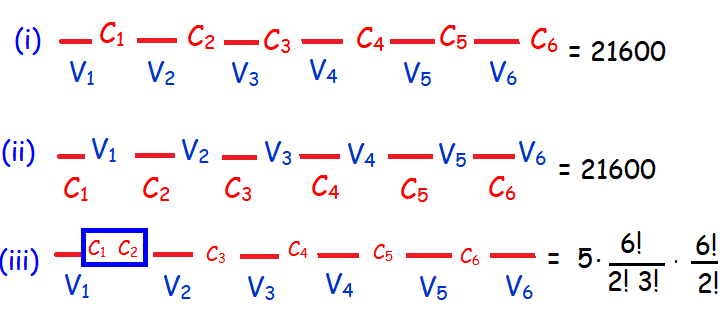
  = 21600 + 21600 + 108000

  =  151200

©All rights reserved. onlinemath4all.com