HOW TO FIND HCF AND LCM EASILY
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Decompose the given numbers into prime factors using ladder division. Then, find the HCF and LCM as explained in the following example.
Find the HCF of 28, 42 and 56.
Use ladder division and decompose 32, 48 and 64 into prime factors until all the three numbers are evenly divisible by a prime number.
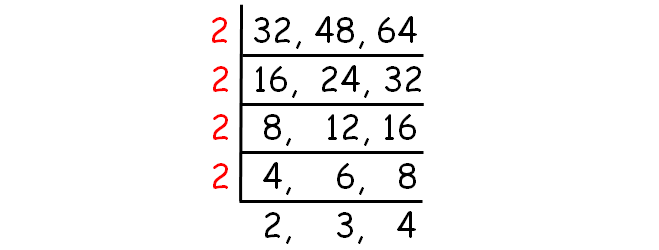
To get HCF, find the product common prime factors of all the three numbers 28, 42 and 56.
HCF of (32, 48, 64) = 2 x 2 x 2 x 2
= 16
Find the LCM of 32, 48 and 64.
Use ladder division and decompose 28, 42 and 56 into prime factors until at least two numbers are evenly divisible by a prime number.
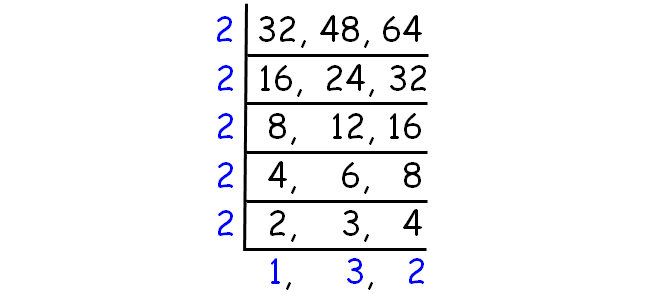
To get LCM, find the product of all prime factors and the numbers in the last row.
LCM of (32, 48, 64) = 2 x 2 x 2 x 2 x 2 x 1 x 3 x 2
= 192
Example 1 :
Find the HCF and LCM of 90 and 30.
Solution :
Decompose 90 and 30 into prime factors using ladder method.
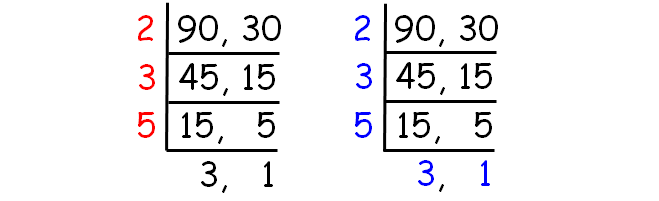
HCF of (90, 30) :
= 2 x 3 x 5
= 30
LCM of (90, 30) :
= 2 x 3 x 5 x 3 x 1
= 90
Example 2 :
Find the HCF and LCM of 105 and 60.
Solution :
Decompose 105 and 60 into prime factors using ladder method.
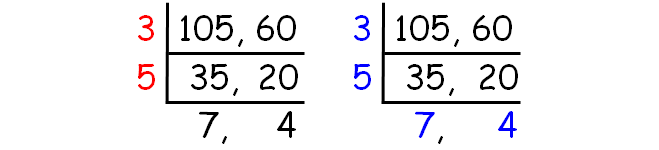
HCF of (105, 60) :
= 2 x 3 x 5
= 30
LCM of (105, 60) :
= 3 x 5 x 7 x 4
= 420
Example 3 :
Find the HCF and LCM of 30 and 50.
Solution :
Decompose 30 and 50 into prime factors using ladder method.
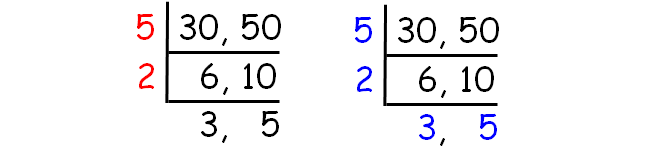
HCF of (30, 50) :
= 5 x 2
= 10
LCM of (30, 50) :
= 5 x 2 x 3 x 5
= 150
Example 4 :
Find the HCF and LCM of 80 and 60.
Solution :
Decompose 80 and 60 into prime factors using ladder method.
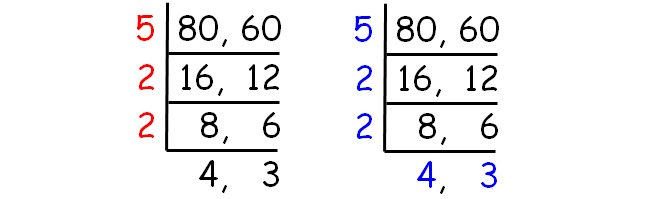
HCF of (80, 60) :
= 5 x 2 x 2
= 20
LCM of (80, 60) :
= 5 x 2 x 2 x 4 x 3
= 240
Example 5 :
Find the HCF and LCM of 36 and 27.
Solution :
Decompose 36 and 27 into prime factors using ladder method.
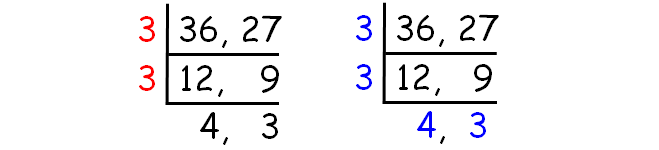
HCF of (36, 27) :
= 3 x 3
= 9
LCM of (36, 27) :
= 3 x 3 x 4 x 3
= 108
Example 6 :
Find the HCF and LCM of 75 and 45.
Solution :
Decompose 75 and 45 into prime factors using ladder method.
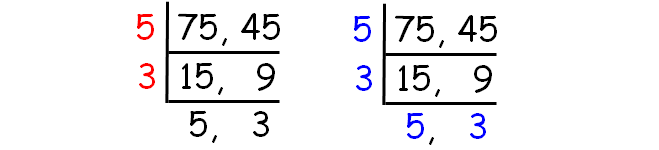
HCF of (75, 45) :
= 5 x 3
= 15
LCM of (75, 45) :
= 5 x 3 x 5 x 3
= 225
Example 7 :
Find the HCF and LCM of 36 and 72.
Solution :
Decompose 36 and 72 into prime factors using ladder method.
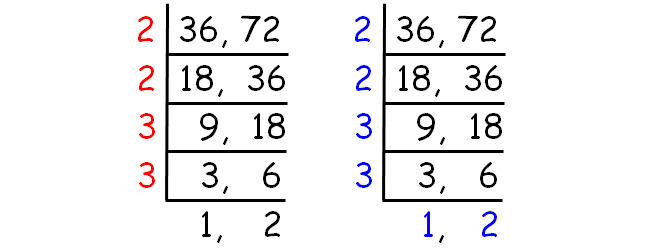
HCF of (36, 72) :
= 2 x 2 x 3 x 3
= 36
LCM of (36, 72) :
= 2 x 2 x 3 x 3 x 1 x 2
= 72
Example 8 :
Find the HCF and LCM of 72 and 63.
Solution :
Decompose 72 and 63 into prime factors using ladder method.
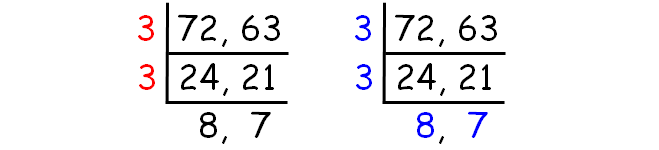
HCF of (72, 63) :
= 3 x 3
= 9
LCM of (72, 63) :
= 3 x 3 x 8 x 7
= 504
Example 9 :
Find the HCF and LCM of 120 and 90.
Solution :
Decompose 120 and 90 into prime factors using ladder method.
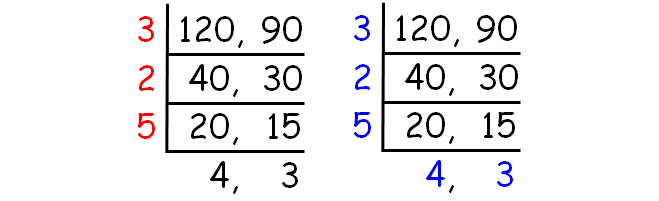
HCF of (120, 90) :
= 3 x 2 x 5
= 30
LCM of (120, 90) :
= 3 x 2 x 5 x 4 x 3
= 360
Example 10 :
Find the HCF and LCM of 45 and 135.
Solution :
Decompose 45 and 135 into prime factors using ladder method.

HCF of (45, 135) :
= 5 x 3 x 3
= 45
LCM of (45, 135) :
= 5 x 3 x 3 x 1 x 3
= 135
Example 11 :
Find the HCF and LCM of 28, 42 and 56.
Solution :
Decompose 28, 42 and 56 into prime factors using ladder method.
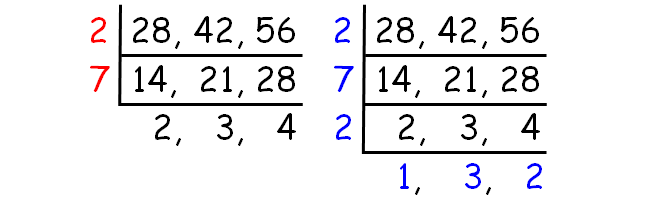
HCF of (28, 42, 56) :
= 2 x 7
= 14
LCM of (28, 42, 56) :
= 2 x 7 x 2 x 1 x 3 x 2
= 168
Example 12 :
Find the HCF and LCM of 45, 55 and 95.
Solution :
Decompose 45, 55 and 95 into prime factors using ladder method.
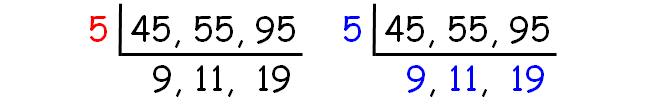
HCF of (45, 55, 95) :
= 5
LCM of (45, 55, 95) :
= 5 x 9 x 11 x 19
= 9405
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Tricky SAT Math Questions with Answers
Feb 25, 26 08:07 AM
10 Tricky SAT Math Questions with Answers -
Solving Exponential Equations
Feb 23, 26 10:06 AM
Solving Exponential Equations - Concept - Examples -
SAT Math Problems on Exponents and Radicals
Feb 21, 26 08:28 PM
SAT Math Problems on Exponents and Radicals
