HOW TO FIND EXPANSION OF LOGARITHMIC FUNCTIONS

Example 1 :

Write the first 4 terms of the logarithmic series

log (1 + 4x)

Solution :

log(1 + x) = x − (x²/2) + (x³/3) − (x⁴/4) + · · ·

Instead of x, apply 4x

log(1 + 4x)  =  4x − [(4x)²/2] + [(4x)³/3] − [(4x)⁴/4] +..........

 =  4x − (16x²/2) + (64x³/3) − (256x⁴/4) +............

 =  4x − 8x² + (64x³/3) − 64x⁴ +............

Required condition is |x| < 1/4

Example 2 :

Write the first 4 terms of the logarithmic series

log(1 − 2x)

Solution :

log(1 − x) = −x − x²/2 − x³/3 − x⁴/4 − ·· ·

Instead of x, apply 2x

log(1 - 2x)  =  -2x − [(2x)²/2] - [(2x)³/3] − [(2x)⁴/4] +..........

 =  -2x − (4x²/2) - (8x³/3) − (16x⁴/4) +............

 =  -2x − 2x² + (8x³/3) − 4x⁴ +............

Required condition is |x| < 1/2

Example 3 :

Write the first 4 terms of the logarithmic series

log [(1+3x)/(1−3x)]

Solution :

log [ (1 + x)/(1 − x)]  = 2 [x + x³/3  + x⁵/5 +............]

Instead of x, apply 3x

log [ (1 + x)/(1 − x)] 

= 2 [3x + (3x)³/3  + (3x)⁵/5 + (3x)⁷/7............]

 = 2 [3x + (27x³/3)  + (243x⁵/5) + (2187x⁷/7)+............]

Required condition is |x| < 1/3

Example 4 :

Write the first 4 terms of the logarithmic series

log [(1-2x)/(1+2x)]

Solution :

log [ (1 - x)/(1 + x)]  = -2 [x + x³/3  + x⁵/5 +............]

Instead of x, apply 2x

log [(1-2x)/(1+2x)]

= -2 [2x + (2x)³/3 + (2x)⁵/5  + (2x)⁷/7 +............]

 = -2 [2x + (8x³/3)  + (32x⁵/5) + (128x⁷/7)+............]

Required condition is |x| < 1/2

Example 5 :

If y = x + x²/2 + x³/3 + x⁴/4 + · · · , then show that x = y − y²/2! + y³/3! − y⁴/4! + · · · .

Solution :

y = x + x²/2 + x³/3 + x⁴/4 + · · · 

Let us take negative signs on both sides.

-y = -(x + x²/2 + x³/3 + x⁴/4 + · · · )

-y  =  -x - x²/2 - x³/3 - x⁴/4 - · · · 

-y  =  log (1 - x)

e^-y  =  1 - x

x =  1 - e^-y

x = 1 - [1 - y/1! + y²/2! - y³/3! + ............]

x  =  1 - 1 + y/1! - y²/2! + y³/3! - ............

x = y/1! - y²/2! + y³/3! - y⁴/3 + ............

Hence proved.

Example 6 :

If p − q is small compared to either p or q, then show that 

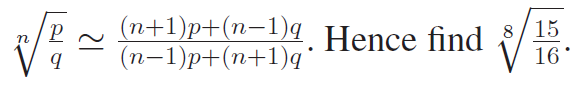
Solution :

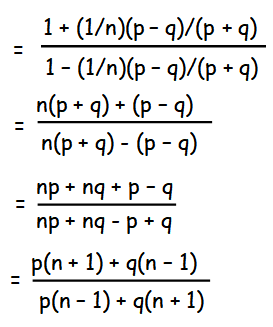
Hence proved.

From this, we have to find the value of 8th root of (15/16)

p = 15, q = 16 and n = 8

  =  [15 (8 + 1) + 16 (8 - 1)]/[15 (8 - 1) + 16 (8 + 1)]

  =  [15 (9)+16(7)]/[15 (7) + 16 (9)]

  =  [135 + 112]/[105 + 144]

  =  247/249 

  =  0.9919

Example 7 :

Find the coefficient of x⁴ in the expansion of (3−4x+x²)/e^2x .

Solution :

e^x  =  1 + x/1! + x²/2! + x³/3! + ..............

(3−4x+x²)/e^2x  =  (3−4x+x²)(1/e^2x)

Expansion for e^x :

1 + x/1! + x²/2! + x³/3! + x⁴/4! ..............

Expansion for e^2x :

1 - 2x/1! + (-2x)²/2! + (-2x)³/3! + (-2x)⁴/4! ..............

1 - 2x/1! + 4x²/2 - 8x³/6 + 16x⁴/24 ..............

  =  (3−4x+x²) (1 - 2x + 2x² - 4x³/3 + 2x⁴/3 ..............)

Coefficient of x⁴

  =  2x⁴ + (16x⁴/3) + 2x⁴

  =  (2 + 16/3 + 2) x⁴

  =  (4 + 16/3)x⁴

  =  28x⁴/3

  =  (28/3)x⁴

Example 8 :

Find the value

Solution :

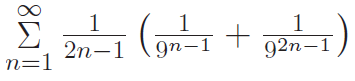
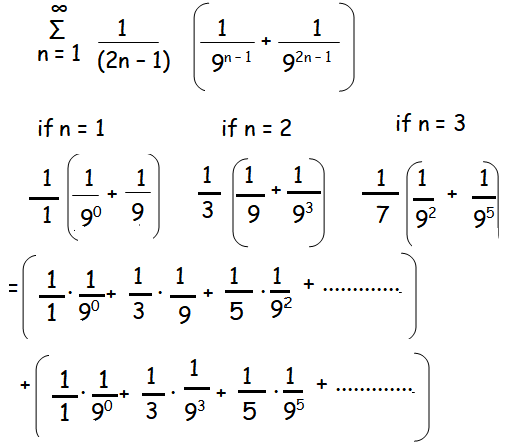
Formula for 

log [(1 + x)/(1 - x)]  =  2 [x + x³/3 + x⁵/5 +..........]

[x + x³/3 + x⁵/5 +..........]  =  (1/2)log [(1 + x)/(1 - x)]

=  (3/2) log(1 + (1/3)/(1-(1/3)) + (1/2)log(1 + (1/9)/(1-(1/9))

=  (3/2) log(4/2) + (1/2)log(10/9)/(8/9)

=  (3/2) log 2 + (1/2) log (5/4)

=  (1/2) log 2³ + (1/2) log (5/4)

=  (1/2) [log 8 + log (5/4)]

=  (1/2) log 10

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.