HOW TO FIND EQUATION OF NORMAL TO THE CURVE

In mathematics the word ‘normal’ has a very specific meaning. It means ‘perpendicular’ or ‘at right angles’.

The normal is then at right angles to the curve so it is also at right angles (perpendicular) to the tangent. 

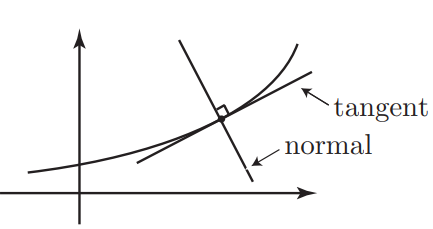
For each of the function given below determine the equation of normal at each of the points indicated.

(i)  f(x)  =  x²+3x+1 at x = 0

(ii)  f(x)  =  tanx at x = π/4 

Question 1 :

 f(x)  =  x² + 3x + 1 at x = 0

Solution :

y  =  f(x)  =  x²+3x+1

When x = 0, then y  =  1

So, we find equation of normal to the curve drawn at the point (0, 1).

When we differentiate the given function, we will get the slope of tangent.

dy/dx  =  f'(x) = 2x + 3 (Slope of tangent)

-1/m  =  -1/(2x+3) (Slope of normal)

Slope of normal at x  =  0.

-1/m  =  -1/3

Equation of normal :

(y-y₁)  =  (-1/m)(x-x₁)

Slope of normal  =  -1/3 and the point (0, 1).

y-1  =  (-1/3)(x-0)

3y-3  =  -1(x)

3y-3  =  -x

x+3y-3  =  0

Question 2 :

f(x)  =  tanx at x = π/4 

Solution :

y  =  f(x)  =  tanx

When x = π/4, then y  =  1

So, we find equation of normal to the curve drawn at the point (π/4, 1).

When we differentiate the given function, we will get the slope of tangent.

dy/dx  =  f'(x)  =  sec²x (Slope of tangent)

-1/m  =  -1/sec²x (Slope of normal)

Slope of normal at x  =  π/4

-1/m  =  -1/(√2)²

-1/m  =  -1/2

Equation of normal :

(y-y₁)  =  (-1/m)(x-x₁)

Slope of normal  =  -1/2 and the point (π/4, 1).

y-1  =  (-1/2)(x-π/4)

2y-2  =  -1(x-π/4)

2y-2  =  -x+π/4

x+2y-2-π/4  =  0

Question 3 :

Find the equation of each normal of the function

f(x)  =  (x³/3)+ x² + x − (1/3)

which is parallel to the line

y  =  (− x/4) + (1/3)

Solution :

f'(x)  =  x²+2x+1

Slope of normal :

-1/f'(x)  =  -1/(x²+2x+1) ---(1)

Normal line is parallel to the given line y = (− x/4) + (1/3)

Slope of the above line  =  -1/4 ---(2)

(1)  =  (2)

 -1/(x²+2x+1)  =  -1/4

x²+2x+1  =  4

x²+2x-3  =  0

(x+3)(x-1)  =  0

x  =  -3 and x  =  1

y  =  f(x)  =  (x³/3)+x²+x−(1/3)

When x  =  -3

y  =  -9+9-3-(1/3)

y  =  -3-(1/3)

y  =  -10/3

When x  =  1

y  =  (1/3)+1+1-(1/3)

y  =  2

The required points (-3, -10/3) and (1, 2).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.