HOW TO FIND DOMAIN AND RANGE OF A FUNCTION WITHOUT GRAPHING

How to find domain and range of a function without graphing ?

Here we are going to see how to find domain and range of a function without graphing.

What is domain ?

The domain of a function is the complete set of possible values of the independent variable.

In other words, the domain of f(x) is the set of all those real numbers for which f(x) is meaningful.

For example, let us consider the function

f(x)  =  (3x - 2)/(x² - 1)

The above function accepts all real values except -1 and 1.If we apply x = 1 and -1, the function will become meaningless.

Hence the domain of the given function is R - {-1, 1}

What is range ?

The range of real function of a real variable is the step of all real values taken by f(x) at points in its domain.

To find the range of the real function, we need to follow the steps given below.

Step 1 :

Put y = f(x)

Step 2 :

Solve the equation y = f(x) for x in terms of y. Let x = g(y)

Step 3 :

Find the values of y for which the values of x, obtained from x = g(y) are real and its domain of f.

Step 4 :

The set of values of y obtained in step 3 is the range of the given function.

Let us look into some example problems to understand the above concept.

Example 1 :

Find the domain and range of the following function

f(x)  =  x / (1 + x²)

Solution :

Domain of the function f (x) :

f(x)  =  x / (1 + x²)

The denominator will never become zero for any values of x.

Thus f(x) accepts all real values of x.

Hence the domain of the given function is R.

Domain of the function f (x) :

y  =  x / (1 + x²)

y (1 + x²)  = x 

y + yx²  = x

x²y - x + y = 0

Solving for x, we get

x = 1 ± √(1 - 4y²) / 2y

Clearly, x will assume real values if 

1 - 4y² ≥ 0 and y ≠ 0

4y² - 1 ≤ 0 and y ≠ 0

Divide by 4 on both sides

y² - 1/4 ≤ 0

y² - (1/2)² ≤ 0

(y - 1/2) (y + 1/2) ≤ 0 and y ≠ 0

-1/2 ≤ y ≤ 1/2 and y ≠ 0

y ∈ [-1/2, 1/2] - {0}

But, in the original function y  =  x / (1 + x²), y = 0 for x = 0. So we have to include "0" in the range.  

Hence, the range of f (x) is [-1/2, 1/2].

Example 2 :

Find the domain and range of the following function

f(x)  =  3 / (2 - x²)

Solution :

Domain of the function f (x) :

f(x)  =  3 / (2 - x²)

To find domain, we need to find out for what values of x the denominator will become zero.

2 - x² = 0

Subtract 2 on both sides

2 - x² - 2  = 0 - 2

- x²   = - 2  ===> x = ± √2

From this, we come to know that the values √2 and -√2 will make the denominator zero.

Hence the domain is R - {± √2}

Range of the function f(x) :

y  =  3 / (2 - x²)

y (2 - x²)  =  3

2y - x² y = 3

2y - 3 = x² y

x²   =  (2y- 3)/y  ==> x = √((2y- 3)/y)

√((2y- 3)/y) ≥ 0

y = 3/2 will make the above term as zero.

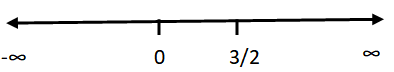
From the above number line, we can split it into three parts.

 (-∞, 0) , (0, 3/2], [3/2, ∞) 

Now we need to apply the values from each intervals. The intervals which satisfies the above condition will be the range.

The values from the intervals  (-∞, 0), [3/2, ∞) satisfies the above condition.

Hence the range of f(x) is  (-∞, 0) U [3/2, ∞).

Example 3 :

Seth’s father is thinking of buying his son a six-month movie pass for $40. Every time he uses the pass, he saves $2. The equation y = 2x – 40 can be used to model the total amount of money that Seth has saved overall in a given month by using the pass, where x is the number of times he uses the pass. What is the domain and range of the function?

Solution :

y = 2x - 40

x is the number of times he uses the pass. He can use the pass many times.

x ≥ 0

Range is -40 ≤ y ≤ ∞

Example 4 :

For babysitting, Nicole charges a flat fee of $3, plus $5 per hour. The equation y = 5x + 3 represents this situation. What is the domain and range of the function?

Solution :

The minimum number of hours to take care of the child is 0 and maximum anything. So, the domain is

0  ≤ x ≤ ∞

The minimum amount to be spent is 3 and maximum may be anything.

3  ≤ y ≤ ∞

Example 5 :

A ball was thrown into the air with an initial velocity of 72 feet per second. The height of the ball after t seconds is represented by the equation h = 72t – 16t² . The graph of the function is shown to the right.

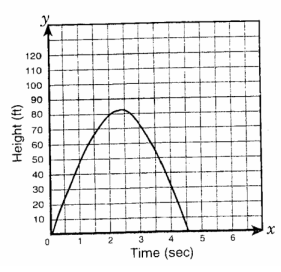
a) Describe the dependent variable for this problem.

b) Describe the domain and range for this problem using appropriate notation. Domain: Range:.

Solution :

a) Time is the independent variable and height is the dependent variable.

b) Domain is 0  ≤ x ≤ 4.5 and range is 0  ≤ x < 85

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.