HOW TO FIND DERIVATIVES USING FIRST PRINCIPLE

How to Find Derivatives Using First Principle :

Here we are going to see how to find derivatives using first principle

Let f be defined on an open interval I ⊆ R containing the point x₀, and suppose that

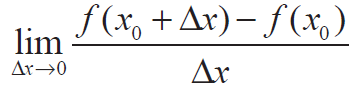
exists. Then f is said to be differentiable at x₀ and the derivative of f at x0, denoted by f'(x₀) , is given by

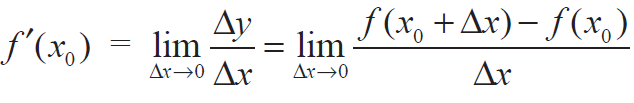
For a function y = f(x) defined in an open interval (a, b) containing the point x₀, the left hand and right hand derivatives of f at x = h are respectively denoted by f'(h^-) and f'(h⁺)

f'(h^-)  =  lim _{h-> 0}^-[f(x + h) - f(x)] / h

f'(h⁺)  =  lim _{h-> 0}⁺[f(x + h) - f(x)] / h

provided the limits exist.

Question 1 :

Find the derivatives of the following functions using first principle.

Solution :

(i) f(x)  =  6

f'(x)  =  lim _{h-> 0}[f(x + h) - f(x)] / h

f(x + h)  =  6

f'(x)  =  lim _{h-> 0}((6) - 6)/h

  =  lim _{h-> 0}  (0/h)

  =  0

(ii)  f(x)  =  -4x + 7

f'(x)  =  lim _{h-> 0}[f(x + h) - f(x)] / h

f(x + h)  =  -4(x + h) + 7

f'(x)  =  lim _{h-> 0}(-4(x + h) + 7 - (-4x + 7))/h

=  lim _{h-> 0}(-4x - 4h + 7 + 4x - 7)/h

  =  lim _{h-> 0}  (-4h/h)

  =  -4

(ii)  f(x)  =  -x² + 2

f'(x)  =  lim _{h-> 0}[f(x + h) - f(x)] / h

f(x + h)  =  -(x + h)² + 2

=  - (x² + h² + 2xh) + 2

=  - x² - h² - 2xh + 2

f'(x)  =  lim _{h-> 0}((- x² - h² - 2xh + 2) - (-x² + 2))/h

 =  lim _{h-> 0}(- x² - h² - 2xh + 2 + x² - 2)/h

 =  lim _{h-> 0}(- h² - 2xh)/h

 =  lim _{h-> 0}(- h - 2x)

  =  -2x

Question 2 :

Find the derivatives from the left and from the right at x = 1 (if they exist) of the following functions. Are the functions differentiable at x = 1?

(i)  f(x)  =  |x - 1|

Solution :

If the function is differentiable, then

f'(1^-)  =  f'(1⁺)

f'(1^-)  =  [f(x) - f(1)] / (x - 1)

=  [-(x - 1) - 0]/(x - 1)

=  -1

f'(1⁺)  =  [f(x) - f(1)] / (x - 1)

=  [(x - 1) - 0]/(x - 1)

=  1

Hence the given function is not differentiable at x = 1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.