HOW TO FIND CUBE ROOT OF A NUMBER

Definition of Cube Root :

Cube root is the inverse process of calculating the cube of a number.

It is denoted by the symbol

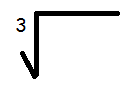
To obtain cube root of a number, we can use the prime factorization method.

Step 1 :

Resolve the given number into prime factors.

Step 2 :

Write these factors in triplets such that all three factors in each triplet are equal.

Step 3 :

From the product of all factors, take one from each triplet that gives the cube root of a number.

Example 1 :

Find the cube root of 512.

Solution :

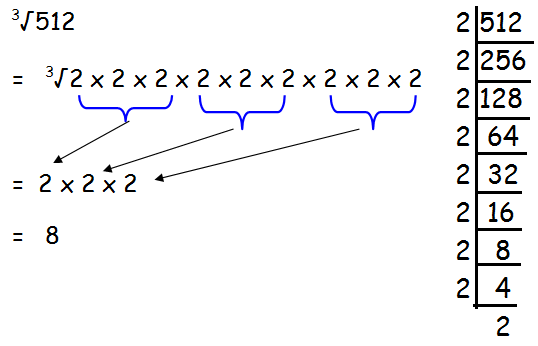
Hence cube root of 512 is 8.

Example 2 :

Find the cube root of 27 x 64.

Solution :

  =  ∛27 x 64 

We can write 27 as 3 x 3 x  3, like wise 64 as 4 x 4 x 4.

  =  ∛3 x 3 x 3 x 4 x 4 x 4

  =  3 x 4

  =  12

Hence the answer is 12.

Example 3 :

Find the cube root of 125/216.

Solution :

Here we need to find the cube root for a fraction. For that, split the numerator and denominator as much as possible.

  =  ∛125/216

125  =  5 x 5 x 5 and 64  =  4 x 4 x 4

  =  ∛(5 x 5 x 5) /(4 x 4 x 4)

Since we have cube root, we need to take one for each three same terms.

  =  5/4

Hence the cube root of 125/216 is 5/4.

Example 4 :

Find the cube root of -512/1000.

Solution :

Here we need to find the cube root for a fraction. In the cube-root we have negative sign.

Whenever we have negative sign inside the cube root, the answer must have negative sign.

  =  ∛512/1000

512  =  8 x 8 x 8 and 1000  =  10 x 10 x 10

  = - ∛(8 x 8 x 8)/(10 x 10 x 10)

Since we have cube root, we need to take one for each three same terms.

  =  - 8/10

If it is possible, we may simplify

  =  - 4/5

Hence the cube root of ∛-512/1000 is -4/5.

Example 5 :

Find the cube root of 0.027.

Solution :

Here we need to find the cube root for a decimal. 

First let us convert the given decimal as fraction. For that, we have to multiply and divide by 1000.

0.027 x  (1000/1000)  =  27/1000

∛0.027  =  ∛27/1000

  =  ∛(3 x 3 x 3)/(10 x 10 x 10)

  =  3/10

Hence the cube root of ∛0.027 is 3/10.

Example 6 :

Find the value of following cube roots:

 ∛(27 × 2744)

Solution :

= ∛(27 × 2744)

Decomposing the numbers as much as possible, we get

= ∛(3 x 3 x 3 x 2 x 2 x 2 x 7 x 7 x 7)

= 3 x 2 x 7

= 42

Example 7 :

By which smallest number must 5400 be multiplied to make it a perfect cube?

Solution :

Decomposing 5400 as much as possible, we get

5400 = 3 x 3 x 3 x 2 x 2 x 5 x 2 x 5 x 2 x 5

= (3 x 3 x 3) x 2 x (2 x 2 x 2) x (5 x 5 x 5)

Grouping as 3 same terms, there is one two extra. By writing two more 2's, we can make it as perfect cube.

So, 4 is the number to be multiplied to make 5400 as perfect square.

Example 8 :

Find the smallest number by which 16384 be divided so that the quotient may be a perfect cube.

Solution :

Decomposing 16384 as much as possible, we get

16384 = 2¹⁴

= 2³ x 2³ x 2³ x 2³ x 2

Grouping as 3 same terms, there is one two extra. So, 2 is the number to be divided to make 16384 as perfect cube.

Example 9 :

Is 4096 a perfect cube? If yes, then what is the number whose cube root is 4096?

Solution :

∛4096 =  ∛2¹²

= ∛(2³ x 2³ x 2³ x 2³)

= 2 x 2 x 2 x 2

= 16

Yes, 4096 is a perfect cube and cube root of 4096 is 16.

Example 10 :

Find the smallest number by which 375 must be multiplied to obtain a perfect cube.

375 = 5 x 5 x 5 x 3

Here we see three same numerals, there is one extra 3. So, 3 is the number to be divided to make 375 as perfect cube.

Example 11 :

Is 53240 a perfect cube? If not, then by which smallest natural number should 53240 be divided so that the quotient is a perfect cube?

Solution :

53240 = 5 x 2 x 2 x 2 x 11 x 11 x 11

By grouping them as product of three same terms, we see one 5 extra. It is not a perfect cube. So, 53240 should be divided by 5 to make it perfect cube.

Example 12 :

Is 68600 a perfect cube? if not, find the smallest number by which 68600 must be multiplied to get a perfect cube

Solution :

68600 = 5 x 5 x 2 x 2 x 2 x 7 x 7 x 7

By grouping the product as set of three same terms. One group which consist of two 5's. So, 5 is the number must be multiplied to make 68600 as perfect cube.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.