HOW TO FIND COMPLEX ROOTS OF A 4TH DEGREE POLYNOMIAL

Example 1 :

Solve the following equation, if (2 + i√3) is a root.

x⁴ - 4x² + 8x + 35 = 0

Solution :

Since (2 + i√3) is a complex root, (2 - i√3) must be the other root.

x = 2 + i√3   or   x - (2 + i√3) = 0

x = 2 - i√3   or   x - (2 - i√3) = 0

Quadratic polynomial with the roots (2 + i√3) and (2 - i√3) :

= x² - (sum of the roots)x + product of the roots

= x² - [(2 + i√3) + (1 - i2√3)]x + (2 + i√3)(2 - i√3)

= x² - [2 + i√3 + 2 - i√3]x + 2² - (√3i)²

= x² - 4x + 4 - (√3)²i²

= x² - 4x + 4 - 3(-1)

= x² - 4x + 4 + 3

= x² - 4x + 7

(x² - 4x + 7) is a factor of (x⁴ - 4x² + 8x + 35).

Let (x² + ax + b) be the other factor.

Then,

(x² + ax + b)(x² - 4x + 7) = x⁴ - 4x² + 8x + 35

Comparing the constant terms,

7b = 35

b = 5

Comparing the coefficient of x terms,

7a - 4b = 8

Substitute b = 5.

7a - 4(5) = 8

7a - 20 = 8

7a = 28

a = 4

x² + ax + b ----> x² + 4x + 5

Solving the equation x² + 4x + 5 = 0, we get

x = -2 + i or -2 - i

Therefore, the roots of the given equation are

2 + i√3, 2 - i√3, -2 + i and -2 - i

Example 2 :

Solve the following equation, if (3 + i) is a root.

x⁴ - 8x³ + 24x² - 32x + 20 = 0

Solution :

Since (3 + i) is a complex root, (3 - i) must be the other root.

x = 3 + i   or   x - (3 + i) = 0

x = 3 - i   or   x - (3 - i) = 0

Quadratic polynomial with the roots (3 + i) and (3 - i) :

= x² - (sum of the roots)x + product of the roots

= x² - [(3 + i) + (3 - i)]x + (3 + i)(3 - i)

= x² - [3 + i + 3 - i]x + 3² - i²

= x² - 6x + 9 - (-1)

= x² - 6x + 9 + 1

= x² - 6x + 10

(x² - 6x + 10) is a factor of (x⁴ - 8x³ + 24x² - 32x + 20).

Let (x² + ax + b) be the other factor.

Then,

(x² + ax + b)(x² - 6x + 10) = x⁴ - 8x³ + 24x² - 32x + 20

Comparing the constant terms,

10b = 20

b = 2

Comparing the coefficient of x terms,

10a - 6b = -32

Substitute b = 2.

10a - 6(2) = -32

10a - 12 = -32

10a = -20

 a = -2

x² + ax + b ----> x² - 2x + 2

Solving the equation x² - 2x + 2 = 0, we get

x = 1 + i or 1 - i

Therefore, the roots of the given equation are

3 + i, 3 - i, 1 + i and 1 - i

Example 3 :

Solve x⁴ – 3x³ + 5x² – 27x – 36 = 0 by finding all roots.

Solution :

Let f(x) = x⁴ – 3x³ + 5x² – 27x – 36 

When x = 1

f(1) = 1⁴ – 3(1)³ + 5(1)² – 27(1) – 36 

= 1 - 3 + 5 - 27 - 36

≠ 0

So, 1 is not the root of the polynomial.

Applying x = -1

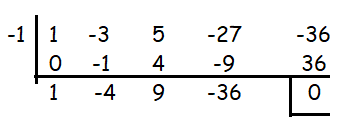
x³ - 4x² + 9x - 36 = 0

x² (x - 4) + 9(x - 4) = 0

(x² + 9)(x - 4) = 0

x² + 9 = 0 and x - 4 = 0

x² = -9 and x = 4

x = ±3i and x = 4

So, the roots are -1, ±3i and 4.

Example 4 :

One root of the cubic equation x³ + px² + 6x + q = 0, where p and q are real is the complex number 5 - i

a) Find the real root of the cubic equation

b)  Find the value of p and q.

Since one of the root is 5 - i then the other root will be 5 + i

Using these two roots, creating a quadratic function, we get

x² - (Sum of roots)x + Product of roots = 0

Sum of roots = 5 + i + 5 - i

= 10

Product of roots = (5 + i)(5 - i)

= 5² - i²

= 25 - (-1)

= 26

So, the required quadratic function is x² - 10x + 26

x³ + px² + 6x + q = (x² - 10x + 26)(x - a)

= x³ - ax² - 10x² + 10ax + 26x - 26a

x³ + px² + 6x + q = x³ - x² (a + 10) + x(10a + 26) - 26a

a + 10 = p ----(1)

10a + 26 = 6 ----(2)

-26a = q ----(3)

from (2), 

10a = 6 - 26

10a = -20

a = -20/10

a = -2

Applying a = -2 in (1), we get

-2 + 10 = p

p = 8

Applying a = -2 in (3), we get

-26(-2) = q

q = 52

a)  x³ + 8x² + 6x + 52 = 0

b) The values of p and q are 8 and 52 respectively.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.