HOW TO FIND APPROXIMATE VALUE USING BINOMIAL EXPANSION

Example 1 :

Find ³√1001 approximately (two decimal places).

Solution :

³√1001  =  (1001)^1/3  =  (1001)^1/3 

  =  (1000 + 1)^1/3

  =  (1000)^1/3 (1 + (1/1000))^1/3

  =  10 (1 + (1/1000))^1/3

  =  10 [1 + (1/3) (1/1000) + ...................]

  =  10 [1 + (0.333)(0.001) ...................] 

  =  10 [1 + 0.000333 ...................] 

  =  10 [1.000333 ...................] 

  =  10.0033..........

Hence the approximate value of ³√1001 is 10.0033..........

Example 2 :

Prove that ³√(x³ + 6) − ³√(x³ + 3) is approximately equal to 1/x² when x is sufficiently large.

Solution :

³√(x³ + 6)  =  (x³ + 6)^1/3  =  (x³)^1/3 [1 + (6/x³)]^1/3

  =  x [1 + (1/3)(6/x³) + ((1/3)(-2/3))/2 (6/x³)² + ..............]

  =  x [1 + (2/x³) + (4/x⁶) + ..............]

  =  x + (2/x²) - (4/x⁵) + ..............   ------(1)

³√(x³ + 3)  =  (x³ + 3)^1/3  =  (x³)^1/3 [1 + (3/x³]^1/3

  =  x [1 + (1/3)(3/x³) + ((1/3)(-2/3)/2)(3/x³)² + ..............]

  =  x [1 + (1/x³) + (-1/x⁶) + ..............]

  =  x + (1/x²) - (1/x⁵) + ..............   ------(2)

³√(x³ + 6) − ³√(x³ + 3)

  =   (x+(2/x²)-(4/x⁵)+ ..............)-(x+(1/x²)-(1/x⁵) + ..............)

  =  x - x + (2/x²) - (1/x²)

  =  1/x²

Example 3 :

Prove that √(1−x)/(1+x) is approximately equal to 1 − x + x² when x is very small.

Solution :

√(1−x)/(1+x)  =  [(1 - x)/(1 + x)]^1/2

=  [(1 - x)^1/2/(1 + x)]^1/2

=  (1 - x)^1/2(1 + x)^-1/2

(1 - x)ⁿ

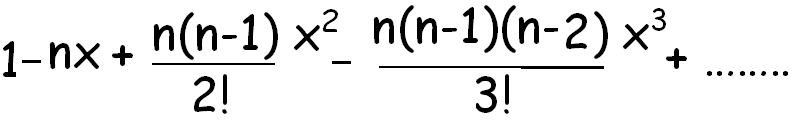
(1 - x)^1/2  =  1 - (1/2)x + ((1/2)(-1/2)/2!)x²+....................

(1 + x)^-1/2  =  1 - (x/2)x - (x²/8)+....................

(1 + x)^-n

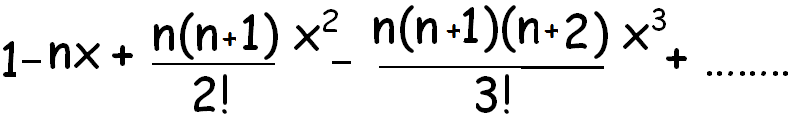
(1 + x)^-1/2  =  1 - (1/2)x + ((1/2)(3/2)/2!)x²+....................

(1 + x)^-1/2  =  1 - (x/2) + (3x²/8) +....................

(1 + x)^-1/2 (1 + x)^-1/2 

  =  (1-(x/2)-(x²/8)+..........)(1 - (x/2)+(3x²/8) +..............)

  = 1 - x/2 + 3x²/8 - x/2 + x²/4 - 3x³/16 - x²/8 + x³/16 +  ..............

  =  1 - [(x/2) + (x/2)] + [(3x²/8) + (x²/4)- (x²/8)

] + .........

  =  1 - x + [(3x²+ 2x²-x²)/8]

  =  1 - x + (4x²/8)

  =  1 - x + x²/2

Hence proved.

Example 4 :

a) Find the first 4 terms of the binomial expansion, in ascending powers of x, of

(1 + x/4)⁸

giving each term in its simplest form.

(b) Use your expansion to estimate the value of (1.025)⁸, giving your answer to 4 decimal places.

Solution :

(x+a)ⁿ = ⁿc₀ x^(n-0) a⁰ + ⁿc₁ x^(n-1) a¹ + ⁿc₂ x^(n-2) a² + ..........

x = 1, a = x/4 and n = 8

a)

Finding first 4 terms of the expansion :

= ⁸c₀ 1^(8-0) (x/4)⁰ + ⁸c₁ 1^(8-1) (x/4)¹ + ⁸c₂ 1^(8-2) (x/4)² + ⁸c₃ 1^(8-3) (x/4)³

= 1⁸ (1) + 8 (1⁷) (x/4) + 28 (1⁶) (x²/16) + 56(1⁵) (x³/64)

= 1 + 2x + (28/16) x² + (56/64) x³

= 1 + 2x + (7/4) x² + (7/8) x³

= 1 + 2x + (7x²/4)  + (7x³/8) 

b) (1.025)⁸ = (1 + 0.025))⁸

Here x/4 = 0.025

x = 0.025(4)

x = 0.1

= 1 + 2(0.1) + (7(0.1)²/4)  + (7(0.1)³/8) 

= 1 + 0.2 + 0.0175 + 0.000875

= 1.2184 (approximately)

Example 5 :

a) Find the first 4 terms of the binomial expansion, in ascending powers of x, of

(1 + x/2)¹⁰

giving each term in its simplest form.

(b) Use your expansion to estimate the value of (1.005)¹⁰, giving your answer to 5 decimal places.

Solution :

(x+a)ⁿ = ⁿc₀ x^(n-0) a⁰ + ⁿc₁ x^(n-1) a¹ + ⁿc₂ x^(n-2) a² + ..........

x = 1, a = x/2 and n = 10

a)

Finding first 4 terms of the expansion :

= ¹⁰c₀ 1^(10-0) (x/2)⁰ + ¹⁰c₁ 1^(10-1) (x/2)¹ + ¹⁰c₂ 1^(10-2) (x/2)² + ¹⁰c₃ 1^(10-3) (x/2)³

= 1¹⁰ (1) + 10 (1⁹) (x/2) + (45/4) x² + 120(1⁷) (x³/8)

= 1 + 5x + (45/4) x² + 15 x³

b) (1.005)¹⁰ = (1 + 0.005))¹⁰

Here x/2 = 0.005

x = 0.005(2)

x = 0.01

= 1 + 5(0.01) + (45/4) (0.01)² + 15 (0.01)³

= 1 + 0.05 + 0.001125 + 0.000015

= 1.05114 (approximately)

Example 6 :

a) Find the first 4 terms of the binomial expansion, in ascending powers of x, of

(1 + ax)¹⁰

where a is a non zero constant. Give each term in its simplest form.

Given that in this expansion, the coefficient of x³ is double the coefficient of x²

b) Find the value of b.

Solution :

(x+a)ⁿ = ⁿc₀ x^(n-0) a⁰ + ⁿc₁ x^(n-1) a¹ + ⁿc₂ x^(n-2) a² + ..........

(1 + ax)¹⁰

x = 1, a = ax and n = 10

a)

Finding first 4 terms of the expansion :

= ¹⁰c₀ 1^(10-0) (ax)⁰ + ¹⁰c₁ 1^(10-1) (ax)¹ + ¹⁰c₂ 1^(10-2) (ax)² + ¹⁰c₃ 1^(10-3) (ax)³

= 1¹⁰ (1) + 10 (1⁹) (ax) + 45 (1⁸) (a²x²) + 120(1⁵) (a³x³)

= 1 + 10 ax + 45a²x² + 120 a³x³

b) Given that,

coefficient of x³ = double the coefficient of x²

120 a³ = 2(45a²)

120 a³ = 90 a²

a = 90/120

a = 3/4

So, the value of a is 3/4.

Example 7 :

a) Find the first 4 terms of the binomial expansion, in ascending powers of x, of

(2 + kx)⁷

where k is a non zero constant. Give each term in its simplest form.

Given that in this expansion, the coefficient of x² is six times the coefficient of x

b) Find the value of k.

Solution :

(x+a)ⁿ = ⁿc₀ x^(n-0) a⁰ + ⁿc₁ x^(n-1) a¹ + ⁿc₂ x^(n-2) a² + ..........

(1 + ax)¹⁰

x = 2, a = kx and n = 7

a)

Finding first 4 terms of the expansion :

= ⁷c₀ 2^(7-0) (kx)⁰ + ⁷c₁ 2^(7-1) (kx)¹ + ⁷c2 2^(7-2) (kx)²+⁷c₃ 2^(7-3) (kx)³

= 2⁷ (1) + 7 2⁶ (kx) + 21 (2⁵) (k²x²) + 35 2⁴ (k³x³)

= 2⁷ + 448 kx + 672 k²x² + 560k³x³

b) Given that,

the coefficient of x² = six times the coefficient of x

672 k² = 6(448 k)

k = 6(448)/672

k = 4

So, the value of k is 4.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.