HOW TO FIND A MATRIX FROM ITS ADJOINT

Formula to Find a Matrix from its Adjoint

If A is a non-singular matrix of order 3, then we get

Question 1 :

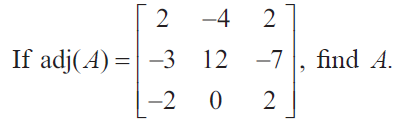
|adj A|  =  2(24 - 0) + 4(-6 - 14) + 2(0 + 24)

  =  2(24) + 4(-20) + 2(24)

  =  48 - 80 + 48

  =  96 - 80

  =  16

√adj A  =  √16  =  4

By applying these values in the formula, we get 

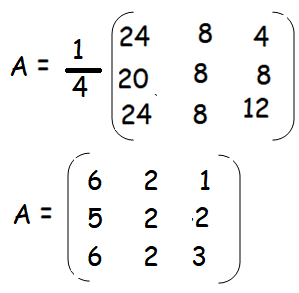
Finding the Inverse of a Matrix Using the Adjoint

Question 2 :

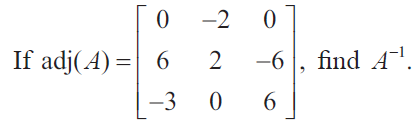
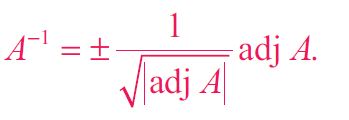
|adj A|  =  0(12 + 0) + 2(36 - 18) + 0(0 + 6)

  =  0 + 2(18) + 0

 |adj A| =  36

√adj A  =  √36  =  6

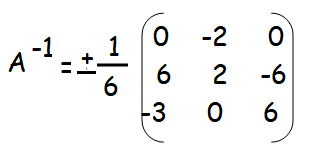
Question 3 :

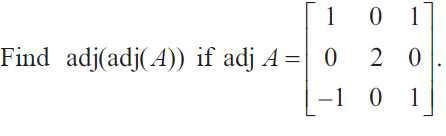
Solution :

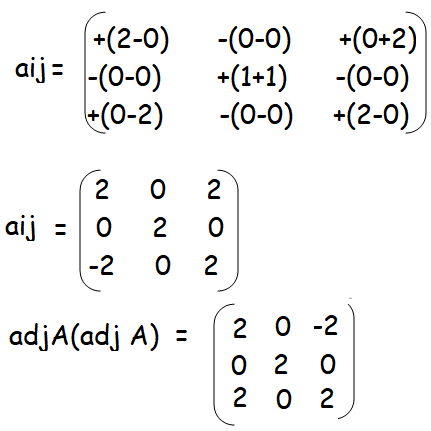
Question 4 :

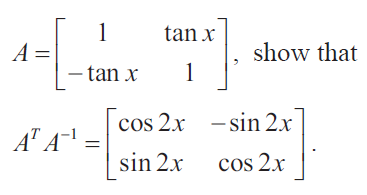
Solution :

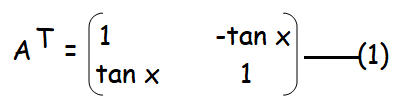
|A|  =  1 + tan² x

|A|  =  sec² x

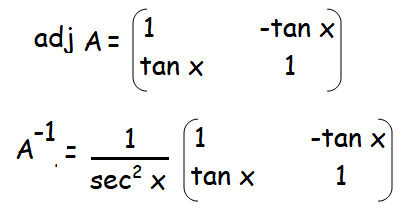
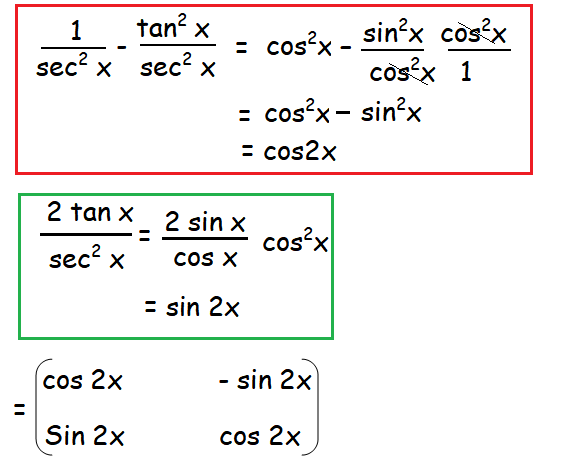
Hence proved.

Question 4 :

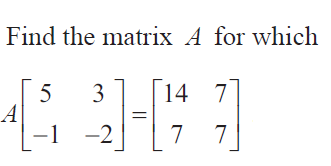
Solution :

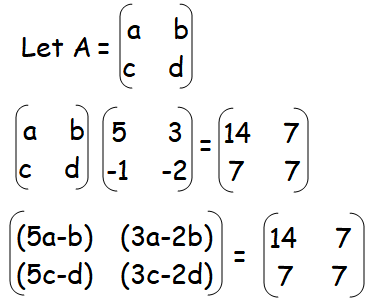
5a - b  =  14  -------(1)

3a - 2b  =  7 -----(2)

(1)x2==> 10a - 2b  =  28

             3a - 2b  =  7

             (-)   (+)    (-)

           -----------------

            7a  =  21

              a  =  21/7  =  3

By applying the value of a in (1), we get

5(3) - b  =  14

-b  =  14 - 15

-b  =  -1

b  =  1

5c - d  =  7  -------(3)

3c - 2d  =  7 -----(4)

(3) x 2  ==>   10c - 2d  =  14

                    3c - 2d  =  7

                   (-)   (+)     (-)

                 -----------------

                   7c  =  7

                    c  =  7/7  = 1

By applying the value of c in (3), we get

5(1) - d  =  7

 5 - d  =  7

-d  =  7 - 5

d  =  -2

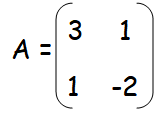
Question 5 :

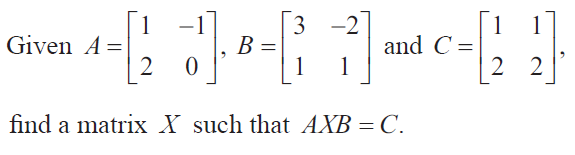
Solution :

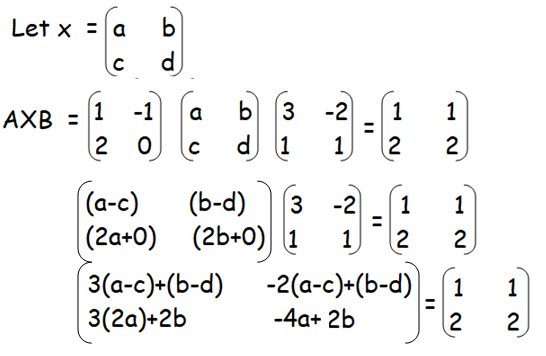
3(a-c)+(b-d)  =  1

3a - 3c + b - d  =  1 ---(1)

-2(a-c)+(b-d)  =  1

-2a+2c + b - d  =  1------(2)

6a + 2b  =  2  ----(3)

-4a + 2b  =  2 -----(4)

(3)/2  ==>  3a + b  =  1

(4)/2  ==> -2a + b  =  1

By subtracting the above equations, we get  

a  =  0

By applying the value of a in (3), we get

3(0) + b  =  1

 b  =  1

From (1),

3a - 3c + b - d  =  1 ---(1)

-3c + 1 - d  =  1

-3c - d  =  1 - 1

-3c - d  =  0 --(A)

From (2),

-2a + 2c + b - d  =  1------(2)

2c + 1 - d  =  1

2c - d  =  1 - 1 

2c - d  =  0--(B)

By solving (A) and (B), we get

(A) - (B)

-3c - 2c  =  0

c  =  0

By applying the value of c in (A), we get 

d  =  0

Question 6 :

Solution :

A^-1  =  (1/|A|) adj A

|A|  =  0(0-1) - 1(0-1) + 1(1-0)

  =  0 + 1 + 1

|A|  =  2

Hence proved.

Question 7 :

Decrypt the received encoded message [2    -3]  [20     4] with the encryption matrix

and the decryption matrix as its inverse, where the system of codes are described by the numbers 1-26 to the letters A− Z respectively, and the number 0 to a blank space.

Solution :

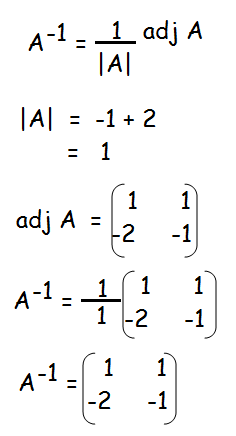
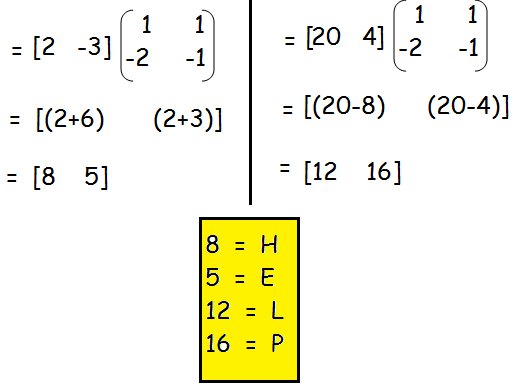
Hence the required word is "HELP".

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.