HOW TO EXPRESS A NUMBER AS THE PRODUCT OF ITS PRIME FACTORS

Example 1 :

Express 324 as the product of its prime factors.

Solution :

Decompose 324 as into prime factors as shown below. 

Product of the prime factors of 324 :

= 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 

  =  2²3⁴

Example 2 :

Express 625 as the product of its prime factors

Solution :

Decompose 625 as into prime factors as shown below. 

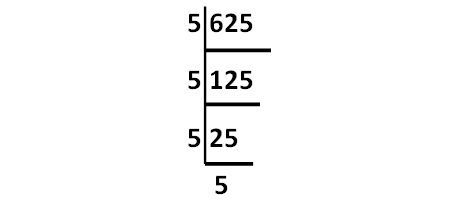
Product of the prime factors of 625 :

  =  5 ⋅ 5 ⋅ 5 ⋅ 5

=  5⁴

Example 3 :

Express 4096 as the product of prime its factors.

Solution :

Decompose 4096 as into prime factors as shown below. 

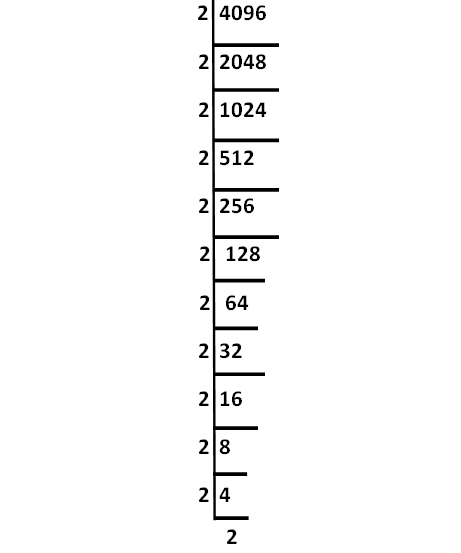
Product of the prime factors of 4096 :

=  2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2

=  2¹²

Example 4 :

Express 400 as the product of its prime factors.

Solution :

Decompose 400 as into prime factors as shown below. 

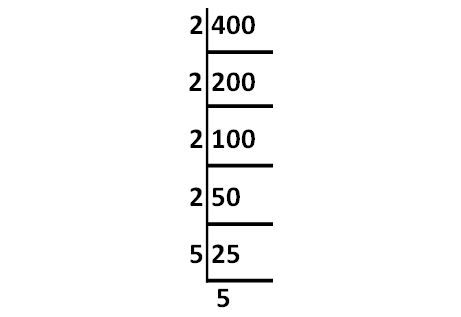
Product of the prime factors of 400 :

=  2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 5 ⋅ 5

=  2⁴5²

Example 5 :

Express 144 as the product of its prime factors

Solution :

Decompose 144 as into prime factors as shown below. 

Product of the prime factors of 144 :

=  2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3

=  2⁴3²

Example 6 :

Express 1024 as the product of its prime factors.

Solution :

Decompose 1024 as into prime factors as shown below. 

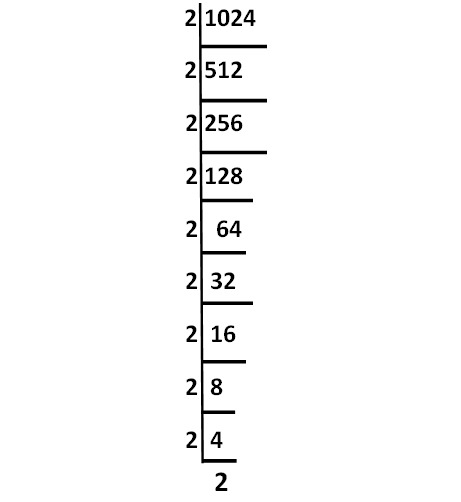
Product of the prime factors of 1024 :

=  2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2

=  2¹⁰

Example 7 :

Express 256 as the product of its prime factors.

Solution :

Decompose 256 as into prime factors as shown below. 

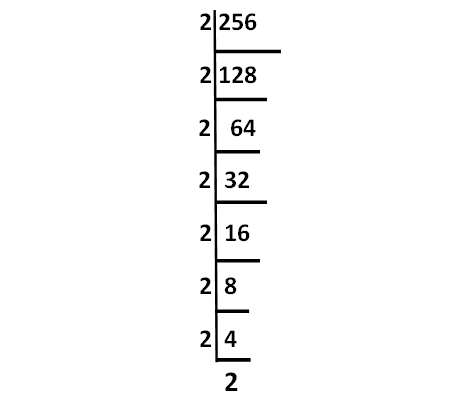
Product of the prime factors of 256 :

=  2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2

=  2⁸

Example 8 :

Express 2025 as the product of its prime factors.

Solution :

Decompose 2025 as into prime factors as shown below. 

Product the prime factors of 2025 :

=  5 ⋅ 5 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3

=  5² 3⁴

Example 9 :

Express 36 as the product of its prime factors

Solution :

Decompose 36 as into prime factors as shown below. 

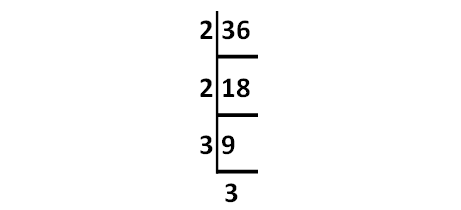
Product of the prime factors of 36 :

=  2 ⋅ 2 ⋅ 3 ⋅ 3

=  2²3²

Example 10 :

Express 3136 as the product of its prime factors.

Solution :

Decompose 3136 as into prime factors as shown below. 

Product of the prime factors of 3136 :

=  2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 7 ⋅ 7

=  2⁶7²

Example 11 :

A number is written as a product of its prime factors as

2 × 3² × 5

Work out the number.

Solution :

= 2 × 3² × 5

= 2 x 3 x 3 x 5

= 90

So, the required number is 90.

Example 12 :

(a) Write 48 as a product of its prime factors.

(b) Find the Highest Common Factor (HCF) of 48 and 56.

Solution :

a)

= 48

= 2 x 2 x 2 x 2 x 3

= 2⁴ x 3

b)

48 = 2⁴ x 3

56 = 2³ x 7

Common factors is 2³. So, 8 is the highest common factor.

Example 13 :

(a) Write 60 as a product of its prime factors.

(b) Find the Lowest Common Multiple (LCM) of 60 and 75

Solution :

a)

60 = 2 x 2 x 3 x 5

= 2² x 3 x 5

Prime factors of 60 is 2² x 3 x 5

b)

60 = 2 x 2 x 3 x 5

= 2² x 3 x 5

75 = 5 x 5 x 3

= 5² x 3

Common and extra factors are 2² x 5² x 3

= 2² x 5² x 3

= 4 x 25 x 3

= 300

So, the highest common factors is 300.

Example 14 :

A teacher divides 36 students into equal groups for a scavenger hunt. Each group should have at least 4 students but no more than 8 students. What are the possible group sizes?

Solution :

Number of students = 36

Dividing into group of 4 :

Number of groups = 36/4

= 9 groups

Dividing into group of 5 :

Number of groups = 36/5

= 7.2 groups (not possible)

Dividing into group of 6 :

Number of groups = 36/6

= 6 groups

Dividing into group of 7 :

Number of groups = 36/7

= not possible

Dividing into group of 8 :

Number of groups = 36/8

= not possible

So, possible number of groups are 9 or 6.

Example 15 :

Is 2 the only even prime number?

Solution :

A prime number will be divisible by 1 and itself. In natural numbers 2 is the number which is divisible by 1 and itself and it is even.

Example 16 :

One table at a bake sale has 75 cookies. Another table has 60 cupcakes. Which table allows for more rectangular arrangements? Explain.

Solution :

Possible ways of decomposing 75 :

75 = 3 x 25

75 = 15 x 5

75 = 75 x 1

Possible ways of decomposing 60 :

60 = 2 x 30

60 = 4 x 15

60 = 6 x 10

60 = 12 x 5

60 = 20 x 3

So, more rectangular of arrangement of 60 is more. Then cupcakes is the answer.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.