HOW TO DRAW FREQUENCY POLYGON
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Frequency Polygon is another method of representing frequency distribution graphically.
Drawing a histogram for the given continuous data :
Mark the middle points of the tops of adjacent rectangles. If we join these middle points successively by line segment, we get a polygon. This polygon is called the frequency polygon. It is customary to bring the ends of the polygon down to base level by assuming a lower class of a frequency and highest class of a frequency.
Frequency Polygon can be constructed in two ways :
(i) Using histogram
(ii) Without using histogram
Construction of Frequency Polygon with Histogram - Steps
Step 1 :
Obtain the frequency distribution from the given data and draw a histogram.
Step 2 :
Join the mid points of the tops of adjacent rectangles of the histogram by means of line segments.
Step 3 :
Obtain the mid points of two assumed class intervals of zero frequency, one adjacent to the first bar on its left and another adjacent to the last bar on its right. These class intervals are known as imagined class interval.
Step 4 :
Complete the polygon by joining the mid points of first and the last class intervals to the mid point of the imagined class intervals adjacent to them.
Example 1 :
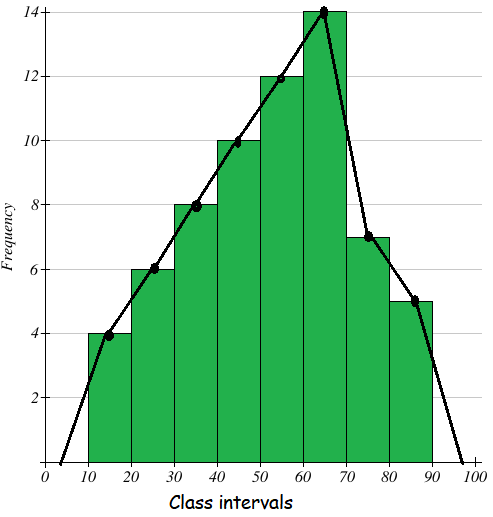
Draw a frequency polygon imposed on the histogram for the following distribution.
|
Class intervals 10 - 20 20 - 30 30 - 40 40 - 50 50 - 60 60 - 70 70 - 80 80 - 90 |
Frequency 4 6 8 10 12 14 7 5 |
Solution :
Take the class-intervals along the X-axis and frequencies along the Y-axis with appropriate scale as shown figure given below.
Draw a histogram for the given data. Now we have to mark the mid points of the upper sides of the consecutive rectangles. We also mark the midpoints of the assumed class intervals 0-10 and 90-100.
The mid points are joined with the help of a ruler. The ends of the polygon are joined with the mid points of 0-10 and 90-100.
Now, we get the frequency polygon.
Scale :
x - axis 1 cm = 10 units
y - axis 1 cm = 2 units
Example 2 :
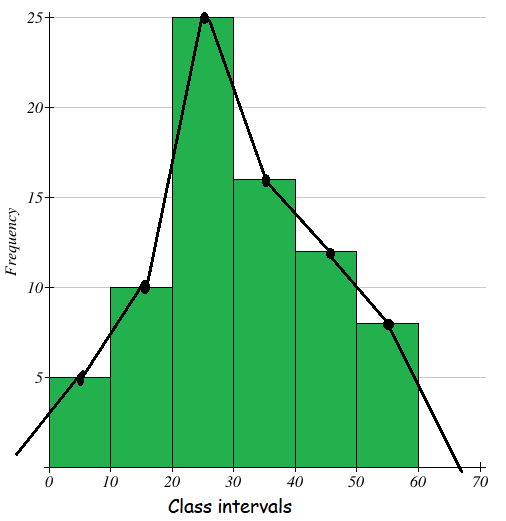
Draw a frequency polygon of the following data using histogram
|
Class intervals 0 - 10 10 - 20 20 - 30 30 - 40 40 - 50 50 - 60 |
Frequency 5 10 25 16 12 8 |
Solution :
Mark the class intervals along the X-axis and the frequencies along the Y-axis with appropriate scale shown in figure given below.
Draw a histogram for the given data. Now, mark the mid points of the upper sides of the consecutive rectangles. Also we take the imagined class interval (-10) - 0 and 60 - 70. The mid points are joined with the help of a ruler. The ends of the polygon are joined with the mid points of the imagined class intervals (-10)-0 and 60 - 70. Now we get the frequency polygon.
Sometimes imagined class intervals do not exist. For example, in case of marks obtained by the students in a test, we cannot go below zero and beyond maximum marks on the two sides.
In such cases, the extreme line segments are only partly drawn and are brought down vertically so that they meet at the mid points of the vertical left and right sides of first and last rectangles respectively.
Example 3 :
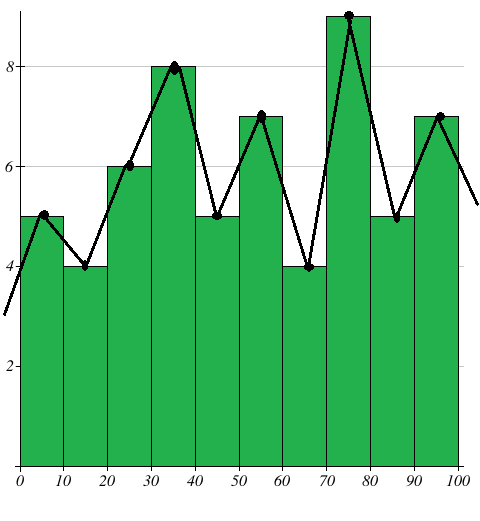
Draw a frequency polygon for the following data using histogram
|
Marks 0 - 10 10 - 20 20 - 30 30 - 40 40 - 50 50 - 60 60 - 70 70 - 80 80 - 90 90 - 100 |
Number of students 5 4 6 8 5 7 4 9 5 7 |
Solution :
Mark the class intervals along the X-axis and the number of students along the Y-axis. Draw a histogram for the given data. Now mark the mid points of the upper sides of the consecutive rectangles. The mid points are joined with the help of a ruler.
Note that, the first and last edges of the frequency polygon meet at the mid point of the vertical edges of the first and last rectangles.
Example 4 :
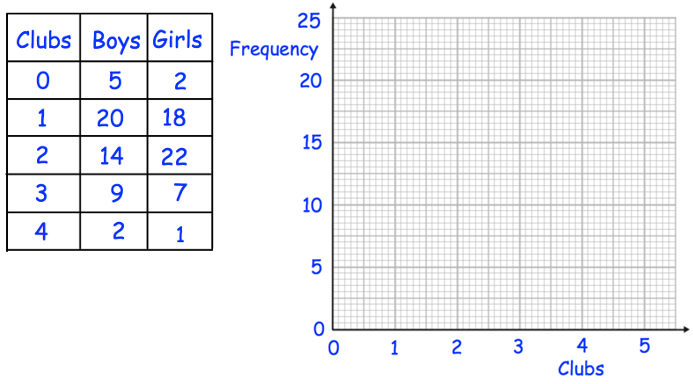
50 boys and 50 girls attend a primary school. The table below shows how many clubs they attend.
(a) On the same grid, draw a frequency polygon for the boys and a frequency polygon for girls.
(b) Compare the distributions.
Solution :
a) By connecting the points (0, 5) (1, 20) (2, 14) (3, 9) and (4, 2), we get the frequency polygon for boys.
b) By connecting the points (0, 2) (1, 18) (2, 22) (3, 7) and (4, 1), we get the frequency polygon for girls.
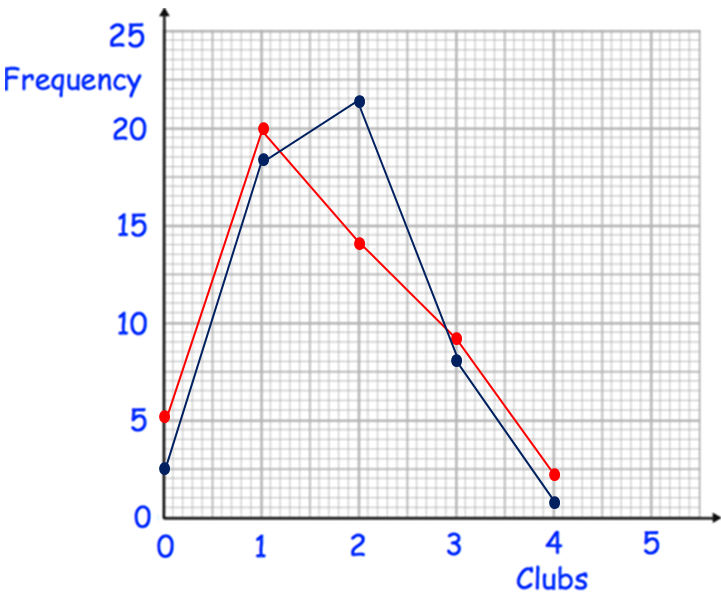
Compare the distributions of the boys and girls. Observe the shapes and central frequency-polygon-q1p1.pngtendencies of the two frequency polygons. The girls' distribution is more skewed towards attending 2 clubs, while the boys' distribution is more skewed towards attending 1 club.
Example 5 :
The frequency polygon shows information about the amount of time people spend in the gym. Calculate an estimate of the mean time spent in the gym.
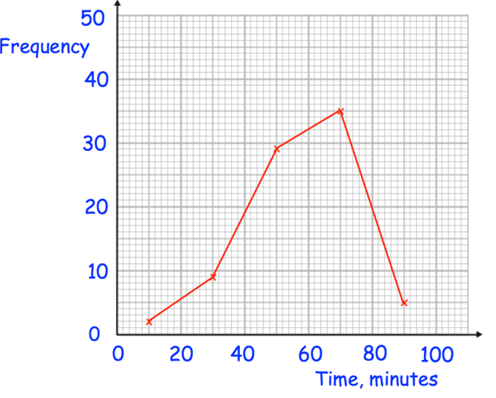
Solution :
(0, 1) (30, 9) (50, 29) (70, 35) (90, 5)
Mean time spent on gym = (1 + 9 + 29 + 35 + 5)/5
= 79/5
= 15.8 minutes
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 06, 26 04:54 AM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

