HOW TO DETERMINE WHETHER THE RELATION IS A FUNCTION

Let f be the rule which maps elements from the set A to set B.

That is, 

f : A ---> B

If a relation is a function, it has to satisfy the following conditions.

(i) Domain of f is A.

(ii) For each x ∈  A, there is only one y ∈ B such that

(x, y) ∈ f

Let us look at some examples to understand how to determine whether a relation is a function or not. 

Example 1 :

Does the following relation represent a function ? Explain.

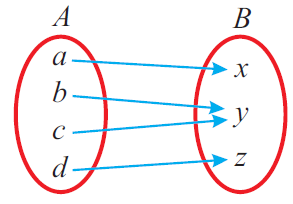
Solution :

Let f be the rule which maps elements from the set A to set B.

Then,

Domain of f  =  {a, b, c, d}  =  A

And also, for each x ∈  A, there is only one y ∈ B. 

So, the above relation is a function. 

Example 2 :

Does the following relation represent a function? Explain.

Solution :

Let f be the rule which maps elements from the set C to set D.

Then,

Domain of f  =  {2, 4, 3}  =  C

For the element '2' in set C, there two images '20' and '40' in D.

So, the above relation is not a function. 

Example 3 :

Let X = {1, 2, 3, 4}. Examine whether the relation given below is a function from X to X. Explain

f  =  {(2, 3), (1, 4), (2, 1), (3, 2), (4, 4)}

Solution :

Domain of f  =  {1, 2, 3, 4}  =  X.

For the element '2' in set X, there two images '3' and '1' in Y.

So, the above relation is not a function. 

Example 4 :

Let A = {1, 4, 9, 16} and B = {–1, 2, –3, –4, 5, 6}. Examine whether the relation given below is a function from A to B. In case of a function, write down its range.

f = {(1, –1), (4, 2), (9, –3), (16, –4)}

Solution :

Domain of f  =  {1, 4, 9, 16}  =  A.

Each element in A has a unique image in B.

That is, no element of A has two or more different images in B. 

So, the above relation is a function. 

Range of f  =  {-1, 2, -3, -4}.

Example 5 :

Let X = {1, 2, 3, 4, 5}, Y = {1, 3, 5, 7, 9}. Examine whether the relation given below is a function from X to Y. In case of a function, write down its range.

If  determine which of the following relations from X to Y are functions? Give reason for your answer. In case of a function, write down its domain, co-domain and range.  

R  =  {(1, 1), (2, 1), (3, 3), (4, 3), (5, 5)}

Solution :

Domain of R  =  {1, 2, 3, 4, 5}  =  X

Each element in A has a unique image in B.

That is, no element of A has two or more different images in B. 

So, the above relation is a function. 

And also, 

Domain  =  {1, 2, 3, 4, 5} 

Range  =  {1, 3, 5}    

Co domain  = { 1, 3, 5, 7, 9 }

Example 6 :

Is the relation 'f' in the diagram shown below a function ? Explain.

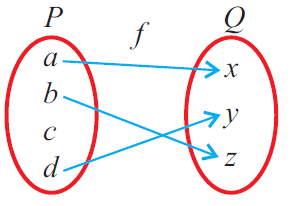
Solution :

From the above arrow diagram,

Domain of f  =  {a, b, d}  ≠  P. 

So, the relation 'f' is not a function.

Example 7 :

Is the relation 'f' in the diagram shown below a function ? Explain.

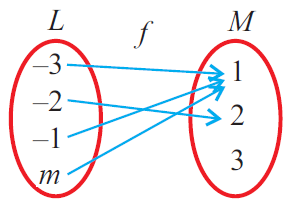
Solution :

From the above arrow diagram,

Domain of f  =  {-3, -2, -1, m}  =  L

Each element in L has a unique image in M.

That is, no element of L has two or more different images in M. 

So, the relation 'f' is a function.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.