HOW TO DETERMINE IN WHICH QUADRANT AN ANGLE LIES

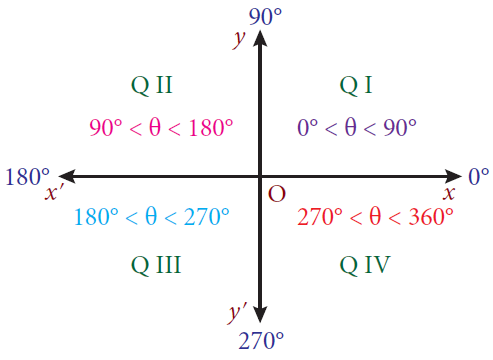
An angle is said to be in standard position if its vertex is at the origin and its initial side is along the positive x-axis.

An angle is said to be in the first quadrant, if in the standard position, its terminal side falls in the first quadrant.

Similarly, we can define for the other three quadrants. Angles in standard position having their terminal sides along the x-axis or y-axis are called quadrantal angles.

Thus, 0°, 90°, 180°, 270° and 360° are quadrantal angles.

Example 1 :

Identify the quadrant in which each of the following  angles lies. 

(i) 25° (ii) 825° (iii) -55° (iv) 328° (v) -230°

Solution :

(i) 25°

Since 25° is between 0 and 90, it is in quadrant I.

(ii) 825°

825° is greater than 360°. 

When 825° is divided by 360°, the remainder is 105°. 

Since 105° is between 90° and 180°, it is in quadrant II. 

That is, 825° is in quadrant II. 

(iii) -55°

Since it is negative angle, we have to do counter clock rotation.

The difference between 360° and 55° is 305°.

Since 305° is between 270° and 360°, it is in quadrant IV. 

So -55° is in quadrant IV. 

(iv) 328°

Since 328° is between 270° and 360°, it is in quadrant IV.

(v) -230°

Since it is negative angle, we have to do counter clockwise rotation. 

The difference between 360° and 230° is 130°.

Since 130° is between 90° and 180°, it is in quadrant II.

So -230° is in quadrant II.

Example 2 :

Name the quadrant the angle lies in.

a) 105°      b) 34°      c) 215°      d) 338°

Solution :

(a) 105°

Since 105° is between 90 and 180, it is in quadrant II.

(b) 34°

Since 34° is between 0 and 90, it is in quadrant I

(c) 215°

Since 215° is between 180 and 270, it is in quadrant III

(d) 338°

Since 338° is between 270 and 360, it is in quadrant IV.

Example 3 :

Name the quadrant the angle lies in.

a) 6𝜋/5     b) 𝜋/5     c) 9𝜋/5     d) 5𝜋/8

Solution :

(a) 6𝜋/5 

6𝜋/5 = 𝜋 + (𝜋/5)

The given angle measure is in the form of 𝜋 +  θ, then it lies in quadrant III.

(b) 𝜋/5

𝜋/5 = 180/5 ==> 36

Since 36° is between 0 and 90, it is in quadrant I

(c) 9𝜋/5

9𝜋/5 = 2𝜋 - (𝜋/5)

So, 9𝜋/5 lies in quadrant IV

(d) 5𝜋/8

5𝜋/8 = 𝜋 - (3𝜋/8)

So, 5𝜋/8 lies in quadrant II.

Example 4 :

Name the quadrant the angle lies in.

a) −235°      b) −94°     c) −345°      d) −138°

Solution :

a) -235 is the negative angle, so we have to move in counter clockwise direction. It lies in -180 to -270, it will lie in quadrant III

b) -94 is the negative angle, so we have to move in counter clockwise direction. It lies in -90 to -180, it will lie in quadrant II

c) -345

It lies in between -270 to -360, it will lie in quadrant IV

d) -138 lies in between -90 to -180, it will lie in quadrant II

Example 5 :

Identify 4 angles, two with positive measures, and two with negative measures that are coterminal with 108° when in standard position.

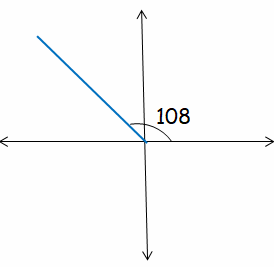
Coterminal angles means the angles begin and end in the same position in the circle. Add complete circles for the positive answers and subtract complete circles for the negative answers.

Since the starting and ending position must be the same, then 

Positive angles :

360 + 108 = 468

2(360) + 108 = 828

Negative angles :

108 - 360 = -252

108 - 2(360) = -612

So, the required angle measures are 468, 828, -252 and -612

Example 6 :

Identify 4 angles, two with positive measures, and two with negative measures that are coterminal with 2𝜋/7 when in standard position.

Solution :

Positive angles :

2𝜋/7 + 2𝜋 ==> (2𝜋 + 14𝜋)/7 ==> 16𝜋/7

2𝜋/7 + 4𝜋 ==> (2𝜋 + 28𝜋)/7 ==> 30𝜋/7

Negative angles :

(2𝜋/7) - 2𝜋 ==> (2𝜋 - 14𝜋)/7 ==>  -12𝜋/7

(2𝜋/7) - 4𝜋 ==> (2𝜋 - 28𝜋)/7 ==> -26𝜋/7

So, the required angles are 16𝜋/7, 30𝜋/7, -12𝜋/7 and -26𝜋/7.

Example 7 :

Express the following as trigonometric ratios of either 30°, 45° or 60°, and hence find their exact values:

(a) sin (− 135°)

(b) cos 225°

(c) tan (− 120°)

(d) sin (− 200°)

Solution :

(a) sin (− 135°)

= - sin 135

The given angle 135 lies in quadrant II. Using reference angle, the angle lies in the II quadrant will be in the form 180 - θ

= - sin (180 - 135)

= - sin 45

= - 1/√2

(b) cos 225°

The given angle 225 lies in quadrant III. Using reference angle, the angle lies in III quadrant will be in the form θ - 180

Using ASTC, cos 225 will be negative.

= -cos (225 - 180)

= -cos 45

= -1/√2

(c) tan (− 120°)

= - tan 120

The given angle 120 lies in quadrant II. Using reference angle, the angle lies in II quadrant will be in the form 180 - θ

Using ASTC, value of tan 120 is negative. 

= tan (180 - 120)

= tan 60

= √2

(d) sin (− 200°)

= - sin (200)

The given angle 200 lies in quadrant III. Using reference angle, the angle lies in III quadrant will be in the form θ - 180

Using ASTC, the value of sin 200 will be negative

= sin (200 - 180)

= sin 20

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.