HOW TO DETERMINE IF A FRACTION IS TERMINATING OR REPEATING

How to Determine if a Fraction is Terminating or Repeating :

In this section, we will learn, how to determine if a fraction is terminating or repeating.

Let us consider the rational number p/q, where q ≠ 0.

If we can write the denominator in terms of 2 and 5, then the rational number p/q will be in the form as shown below.  

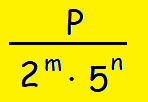
If p ∈ Z and m, n ∈ W, then the rational number will have a terminating decimal expansion.

Otherwise, the rational number will have a non-terminating and recurring decimal expansion.

That is, if the denominator can't be written in terms of 2 and 5, then the rational number p/q will have a non-terminating and recurring decimal expansion.

The following examples will illustrate the concept explained above.

How to Determine if a Fraction is Terminating or Repeating - Examples

Example 1 :

Without actual division, classify the decimal expansion of the following numbers as terminating or non-terminating and recurring.

7 / 16

Solution :

16  =  2⁴

7 / 16  =  7 / (2⁴ ⋅ 5⁰) 

Since the given fraction is in the form p/(2^m ⋅ 5ⁿ), it has terminating  decimal expansion.

Example 2 :

 13 / 150

Solution :

150  =  2 ⋅ 3 ⋅ 5²

13 / 150  =  13 / (2 ⋅ 3 ⋅ 5²) 

Since the given fraction 13/150 is not in the form p/(2^m ⋅ 5ⁿ), it has non terminating  and recurring decimal expansion.

Example 3 : 

-11 / 75

Solution :

75  =   3 ⋅ 5²

-11 / 75  =  -11 / (3 ⋅ 5²) 

Since the given fraction -11 / 75 is not in the form p/(2^m ⋅ 5ⁿ), it has non terminating  and recurring decimal expansion.

Example 4 :

17 / 200

Solution :

200  =   2³ ⋅ 5²

17 / 200  =  17 / (2³ ⋅ 5²) 

Since the given fraction 17/200 is in the form p/(2^m ⋅ 5ⁿ), it has terminating decimal expansion.

Example 5 :

 5 / 64

Solution :

64  =   2⁶ 

5 / 64  =  5 / (2⁶ ⋅ 5⁰) 

Since the given fraction 5 / 64 is in the form p/(2^m ⋅ 5ⁿ), it has terminating decimal expansion.

Example 6 :

11 / 12

Solution :

12  =   2² ⋅ 3

11 / 12  =  11 / (2² ⋅ 3) 

Since the given fraction 11 / 12 is not in the form p/(2^m ⋅ 5ⁿ), it has non terminating and recurring decimal expansion.

Example 7 :

27 / 40

Solution :

40  =   2³ ⋅ 5

27 / 40  =  27 / (2³ ⋅ 5) 

Since the given fraction 27 / 40 is in the form p/(2^m ⋅ 5ⁿ), it has terminating decimal expansion.

After having gone through the stuff given above, we hope that the students would have understood, how to determine if a fraction is terminating or repeating. 

Apart from the stuff given on this web page, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.