HOW TO CONSTRUCT A TRIANGLE WHEN TWO ANGLES AND ONE SIDE IS GIVEN

The way of constructing a triangle is depending on the information given. Here we are going to see, how to construct a triangle when two angles and one side is given.

To construct a triangle when two angles and one side are given, we must need the following mathematical instruments.

1. Ruler

2. Protractor

The steps for the construction of a triangle, when two angles and one side is given.

Construct a triangle XYZ given that XY = 6 cm, ∠ZXY = 30° and ∠XYZ = 100°. Examine whether the third angle.

Given measurements :

XY = 6 cm

∠ZXY = 30°

∠XYZ = 100°

Step 1 :

Draw the line segment XY = 6cm.

Step 2 :

Using protractor, at X, draw a ray XP making an angle of 30° with XY.

Step 3 :

Using protractor, at Y, draw another ray YQ making an angle of 100° with XY. The rays XP and YQ intersect at Z.

Step 4 :

Using the property, "Sum of the three angles of any triangle is 180°", we can find the third angle which is 50°. That is, ∠Z = 50°.

Now, XYZ is the required triangle.

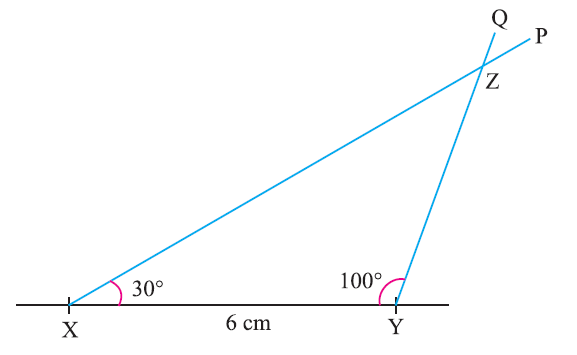
This construction clearly shows how to construct a triangle with the mathematical instruments ruler and protractor when two angles and one side are given.

If lengths of all the three sides are given, can always we construct a triangle?

Let us get answer for the above question with an example.

A student attempted to draw a triangle with given measurements PQ = 2cm, QR = 6cm, PR = 3 cm. First he drew QR = 6cm. Then he drew an arc of 2cm with Q as center and he drew another arc of radius 3 cm with R as center. They could not intersect each to get P.

What is the reason ?

Given measurements :

PQ = 4cm

QR = 6 cm

PR = 3 cm

Step 1 :

Draw a line segment QR = 6cm.

(Here we take the longest side).

Step 2 :

With ‘R’ as center, draw an arc of radius 3 cm above the line QR.

Step 3 :

With ‘Q’ as center, draw an arc of c cm above the line QR

Step 4 :

Now, the arc said in step 2 and arc said in step 3 must intersect.

Let us apply the above steps and see whether the two arcs intersect.

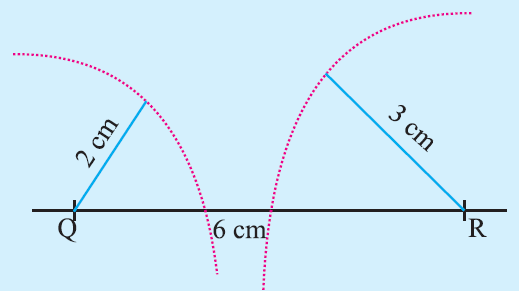
In the above figure, the two arcs said in step 2 and step 3 do not intersect.

Since the two arcs do not intersect, we can not draw a triangle with the given the three sides.

Reason :

According to the property of triangles, we have that he sum of any two sides of a triangle is always greater than the third side.

But here, the sum of the two sides 2 and 3 is less than the third side 6.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.