HOW TO CHECK WHETHER THE GIVEN POINTS FORM A RIGHT TRIANGLE
The following steps would be useful to check whether the given points form a right triangle.
Step 1 :
Using distance formula to find the length of each side of the triangle.
d = √[(x2 - x1)2 + (y2 - y1)2]
Step 2 :
Check Pythagorean Theorem for the lengths of the sides.
That is, square of the larger side has to be equal to sum of the squares of other two sides.
Step 3 :
Decision making :
If the lengths of the sides satisfy Pythagorean Theorem, then the points will form a right triangle, otherwise they won't.
In each case, examine whether the points form a right triangle.
Example 1 :
A(-3, -4), B(2, 6), C(-6, 10)
Solution :
Distance between the points A and B :
AB = √[(x2 - x1)2 + (y2 - y1)2]
Substitute (x1, y1) = (-3, -4) and (x2, y2) = (2, 6).
= √[(2 + 3)2 + (6 + 4)2]
= √[52 + 102]
= √[25 + 100]
= √125
Distance between the points B and C :
BC = √[(-6 - 2)2 + (10 - 6)2]
= √[(-8)2 + 42]
= √[64 + 16]
= √80
Distance between the points A and C :
= √[(-6 + 3)2 + (10 + 4)2]
= √[(-3)2 + 142]
= √[9 + 196]
= √205
|
AC2 = (√205)2 = 205 ----(1) |
AB2 + BC2 = (√125)2 + (√80)2 = 125 + 80 = 205 ----(2) |
From (1) and (2),
AC2 = AB2 + BC2
The points A, B and C form a right triangle.
Example 2 :
P(7, 1), Q(-4, -1), R(4, 5)
Solution :
Distance between the points P and Q :
PQ = √[(-4 - 7)2 + (-1 - 1)2]
= √[(-11)2 + (-2)2]
= √[121 + 4]
= √125
Distance between the points Q and R :
QR = √[(4 + 4)2 + (5 + 1)2]
= √[82 + 62]
= √[64 + 36]
= √100
Distance between the points P and R :
PR = √[(4 - 7)2 + (5 - 1)2]
= √[(-3)2 + 42]
= √[9 + 16]
= √25
|
PQ2 = (√125)2 = 125 ----(1) |
QR2 + PR2 = (√100)2 + (√25)2 = 100 + 25 = 125 ----(2) |
From (1) and (2),
PQ2 = QR2 + PR2
The points P, Q and R form a right triangle.
Example 3 :
P(4, 4), Q(3, 5), R(-1, -1)
Solution :
Distance between the points P and Q :
PQ = √[(3 - 4)2 + (5 - 4)2]
= √[(-1)2 + 12]
= √[1 + 1]
= √2
Distance between the points Q and R :
QR = √[(-1 - 3)2 + (-1 - 5)2]
= √[(-4)2 + (-6)2]
= √[16 + 36]
= √52
Distance between the points P and R :
PR = √[(-1 - 4)2 + (-1 - 4)2]
= √[(-5)2 + (-5)2]
= √[25 + 25]
= √50
|
QR2 = (√52)2 = 52 ----(1) |
PQ2 + PR2 = (√2)2 + (√50)2 = 2 + 50 = 52 ----(2) |
From (1) and (2),
QR2 = PQ2 + PR2
The points P, Q and R form a right triangle.
Example 4 :
A(2, 0), B(-2, 3), C(-2, -5)
Solution :
Distance between the points A and B :
= √[(-2 - 2)2 + (3 - 0)2]
= √[(-4)2 + 32]
= √[16 + 9]
= √25
Distance between the points B and C :
BC = √[(-2 + 2)2 + (-5 - 3)2]
= √[0 + (-8)2]
= √64
Distance between the points A and C :
= √[(-2 - 2)2 + (-5 - 0)2]
= √[(-4)2 + (-5)2]
= √[16 + 25]
= √41
|
BC2 = (√64)2 = 64 ----(1) |
AB2 + AC2 = (√25)2 + (√41)2 = 25 + 41 = 66 ----(2) |
From (1) and (2),
BC2 ≠ AB2 + AC2
Since Pythagorean theorem is not satisfied, the points A, B and C do not form a right triangle.
Example 5 :
A(0, 0), B(5, 0), C(0, 6)
Solution :
Distance between the points A and B :
= √[(5 - 0)2 + (0 - 0)2]
= √[52 + 0]
= √25
Distance between the points B and C :
BC = √[(0 - 5)2 + (6 - 0)2]
= √[(-5)2 + 62]
= √[25 + 36]
= √61
Distance between the points A and C :
A(0, 0) C(0, 6)
= √[(0 - 0)2 + (6 - 0)2]
= √[02 + 62]
= √36
|
BC2 = (√61)2 = 61 ----(1) |
AB2 + AC2 = (√25)2 + (√36)2 = 25 + 36 = 61 ----(2) |
From (1) and (2),
BC2 = AB2 + AC2
The points A, B and C form a right triangle.
Example 6 :
You ride your bicycle along the outer edge of a park. Then you take a shortcut back to where you started. Find the length of the shortcut. Round your answer to the nearest tenth.
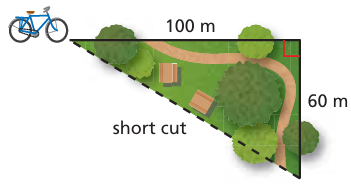
Solution :
To find the length of shortcut, we have to find the hypotenuse.
Let x be the length of shortcut.
x2 = 1002 + 602
= 10000 + 3600
Length of shortcut = 13600
= √13600
= 116.6 m
So, the required length of shortcut is 117 m
Tell whether the triangle with the given side lengths is a right triangle.
Example 7 :
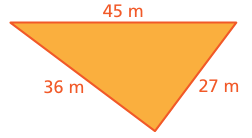
Solution :
452 = 45 x 45 ==> 2025
362 = 36 x 36 ==> 1296
272 = 27 x 27 ==> 729
2025 = 1296 + 729
2025 = 2025
So, the given measures are measures of right triangle.
Example 8 :
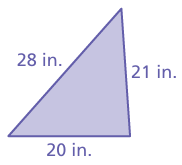
Solution :
282 = 28 x 28 ==> 524
212 = 21 x 21 ==> 441
202 = 20 x 20 ==> 400
524 = 441 + 400
524 ≠ 841
So, the given measures are not the measures of right triangle.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 213)
Jul 13, 25 09:51 AM
Digital SAT Math Problems and Solutions (Part - 213) -
Digital SAT Math Problems and Solutions (Part - 212)
Jul 13, 25 09:32 AM
Digital SAT Math Problems and Solutions (Part - 212) -
Digital SAT Math Problems and Solutions (Part - 211)
Jul 11, 25 08:34 AM
Digital SAT Math Problems and Solutions (Part - 211)
