HOW TO CHECK IF THE FUNCTION IS BIJECTIVE

Here we are going to see, how to check if function is bijective.

If a function f : A -> B is both one–one and onto, then f is called a bijection from A to B.

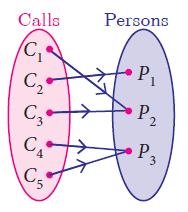
One to One Function

A function f : A -> B is called one – one function if distinct elements of A have distinct images in B.

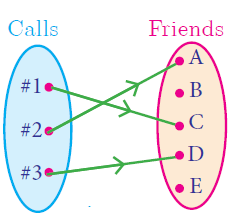
Onto Function

A function f : A -> B is said to be onto function if the range of f is equal to the co-domain of f.

How to Prove a Function is Bijective without Using Arrow Diagram ?

Question 1 :

In each of the following cases state whether the function is bijective or not. Justify your answer.

(i) f : R -> R defined by f (x) = 2x +1

Solution :

Testing whether it is one to one :

If for all a₁, a₂ ∈ A, f(a₁) = f(a₂) implies a₁ = a₂ then f is called one – one function.

Let x, y ∈ R, f(x)  =  f(y)

f(x)  =  2x + 1  ------(1)

f(y)  =  2y + 1  ------(2)

(1) = (2)

2x + 1  =  2y + 1

2x  =  2y 

x  =  y

So, it is one to one.

Testing whether it is onto :

Range of f = co-domain

If f : A -> B is an onto function then, the range of f = B . That is, f(A) = B.

Let x ∈ A, y ∈ B and x, y ∈ R. Then, x is pre-image and y is image. 

Then, we have 

y  =  2x + 1

Solve for x. 

x  =  (y - 1) /2

Here, y is a real number. When we subtract 1 from a real number and the result is divided by 2, again it is a real number. 

For every real number of y, there is a real number x.  

So, range of f(x) is equal to co-domain.

It is onto function.

Hence it is bijective function.

(ii) f : R -> R defined by f (x) = 3 – 4x²

Solution :

Testing whether it is one to one :

If for all a₁, a₂ ∈ A, f(a₁) = f(a₂) implies a₁ = a₂ then f is called one – one function.

Let x, y ∈ R, f(x)  =  f(y)

f(x)  =  3 – 4x²  ------(1)

f(y)  =   3 – 4y²  ------(2)

(1) = (2)

 3 – 4x²  =   3 – 4y²

-4x²  =  –4y²

x² - y² =  0

(x - y)(x + y) =  0

x - y = 0  (or) x + y =  0

x = y (or) x = -y

It is not one to one.Hence it is not bijective function.

Question 2 :

Let A = {−1, 1}and B = {0, 2} . If the function f : A -> B defined by f(x) = ax + b is an onto function? Find a and b.

Solution :

f(x) = ax + b

f(-1) = a(-1) + b  = 0

-a + b  =  0  ------(1)

f(1) = a(1) + b  = 2

a + b  =  2  ------(2)

(1) + (2)

2b  =  2

b  =  1

By applying the value of b in (1), we get

-a + 1  =  0

-a  =  -1

a  =  1

Hence the values of a and b are 1 and 1 respectively.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.