HOW TO CHECK IF PAIR OF STRAIGHT LINES INTERSECT

Here we are going to see how to check if pair of straight lines intersect.

If the given pair of straight lines ax² + 2hxy + by² + 2gx + 2fy + c = 0 intersect each other, then it must satisfy the condition given below.

abc + 2fgh - af² - bg² - ch²  =  0

Point of intersection :

P(hf − bg/ab − h² , gh − af/ab − h²)

How to Check if Pair of Straight Lines Intersect - Questions

Question 1 :

Show that the equation 2x² −xy−3y² −6x + 19y − 20 = 0 represents a pair of intersecting lines. Show further that the angle between them is tan⁻¹(5).

Solution :

2x² −xy−3y² −6x + 19y − 20 = 0

ax² + 2hxy + by² + 2gx + 2fy + c = 0 

a  =  2, h  =  -1/2, b  =  -3, g  =  -3, f = 19/2, c = -20

Condition for intersection of two lines :

abc + 2fgh - af² - bg² - ch²  =  0

2(-3)(-20)+2(19/2)(-3)(-1/2)-2(19/2)²-(-3)(-3)²-(-20)(-1/2)²  =  0

  =  120 + 57/2 - 2(361/4) + 27 + 20(1/4)

  =  120 + 57/2 - 361/2 + 27 + 5

  =  (240 + 57 - 361 + 54 + 10)/2

  =  (361 - 361) / 2

  =  0

Since it satisfies the above condition, the given pair of straight line is intersected.

Now let us find the angle between them.

 θ =  tan^-1 |2√(h²- ab)/(a + b)|

 θ =  tan^-1 |2√(-1/2)²- 2(-3)/(2 + (-3))|

  =  tan^-1 |2√((1/4) + 6)/(-1)|

  =  tan^-1 |2√(25/4)|

  =  tan^-1 |(2(5)/2)|

  =  tan^-1 5

Hence proved.

Question 2 :

Prove that the equation to the straight lines through the origin, each of which makes an angle α with the straight line y = x is x² − 2xy sec 2α + y² = 0

Solution :

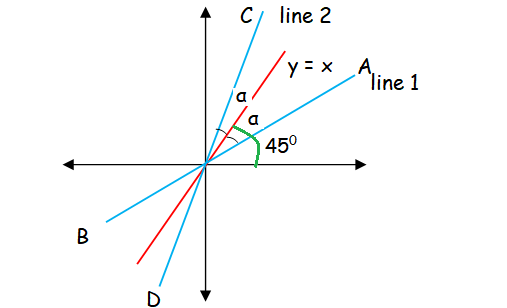
Equation of the line AB :

y  =  m₁ x

m₁ x - y  =  0

Equation of the line CD :

y  =  m₂ x

m₁₂ x - y  =  0

In order to find the slope of first line, let us find the angle between x-axis and the line AB.

θ  =  45 - α   

m₁  =  tan θ  =  tan (45 - α)  ---(1)

Angle between the line CD and x-axis

θ  =  45 + α   

m₂  =  tan θ  =  tan (45 + α)  ---(2)

tan (45 - α)  =  (tan 45 - tan α)/(1 + tan 45 tan α)

m₁  =  (1 - tan α)/(1 + tan α)

tan (45 + α)  =  (tan 45 + tan α)/(1 - tan 45 tan α)

m₂  =  (1 + tan α)/(1 - tan α)

Equation of straight lines :

(m₁ x - y) (m₂ x - y)  =  0

m₁m₂ x²-m₁xy - m₂xy  + y² =  0

m₁m₂ x² - xy(m₁ + m₂) + y² =  0   ----(3)

m₁ + m₂  =  (1 - tan α)/(1 + tan α) + (1 + tan α)/(1 - tan α)

  =  ((1 - tan α)² + (1 + tan α)²)/(1 + tan α)(1 - tan α)

  =  (1 - 2tan α + tan ²α + 1 + 2tan α + tan ²α)/(1-tan²α)

  =  (2 + 2tan ²α)/(1-tan²α)

  =  2[(1+tan²α)/(1-tan²α)]

  =  2 sec 2α

Note :

cos 2α  =  (1-tan²α) / (1+tan²α)

m₁ m₂  =  ((1 - tan α)/(1 + tan α)) ((1 + tan α)/(1 - tan α))

  =  1

By applying the above values in equation 3, we get the required equation.

(1) x² - xy 2 sec 2α + y² =  0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.