HOW TO CHECK IF GIVEN FOUR POINTS FORM A RECTANGLE

Example 1 :

Check whether the following four points form a rectangle.

A(-3, -3), B(4, -3), C(4, 2), D(-3, 2)

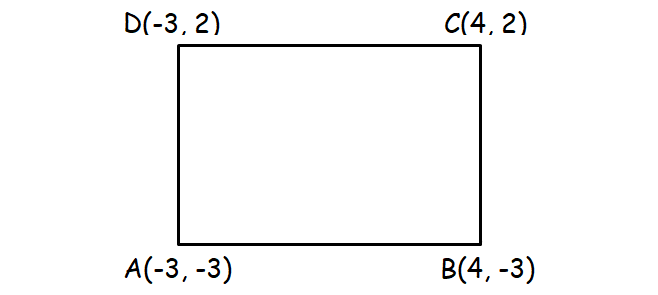
Solution :

Distance between A and B :

Formula to find the distance between two points :

d = √[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁) = A(-3, -3) and (x₂, y₂) = B(4, -3).

= √[(4 + 3)² + (-3 + 3)²]

= √[7² + 0]

= √49

AB = 7 units

Distance between D and C :

= √[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁) = D(-3, 2) and (x₂, y₂) = C(4, 2).

= √[(4 + 3)² + (2 - 2)²]

= √[7² + 0]

= √49

DC = 7 units

Distance between A and D :

= √[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁) = A(-3, -3) and (x₂, y₂) = D(-3, 2).

= √[(-3 + 3)² + (2 + 3)²]

= √[0 + 5²]

= √25

AD = 5 units

Distance between B and C :

= √[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁) = B(4, -3) and (x₂, y₂) = C(4, 2).

= √[(4 - 4)² + (2 + 3)²]

= √[0 + 5²]

= √25

BC = 5 units

From the above workings, AB = DC and AD = BC. 

Opposite sides are equal. 

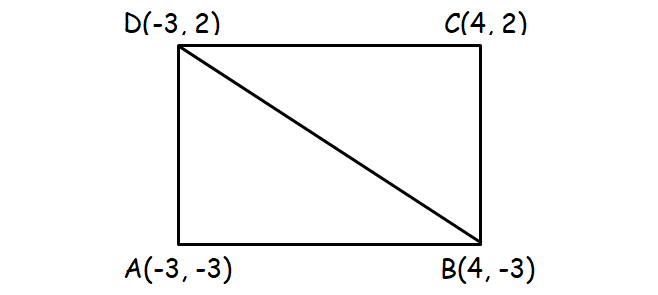
In the diagram above, consider ΔABC. 

Distance between B and D :

= √[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁) = B(4, -3) and (x₂, y₂) = D(-3, 2).

= √[(-3 - 4)² + (2 + 3)²]

= √[49 + 25]

BD = √74

BD² = 74

AB = 7 ----> AB² = 49

AD = 5 ----> AD² = 25

49 + 25 = 74

AB² + AD² = BD²

ΔABC above satisfies Pythagorean Theorem, hence ΔABC is a right triangle with ∠A = 90°. 

Opposite sides are equal and it is proved that one of the vertices has right angle.

So, the given four points form a rectangle. 

Example 2 :

The rectangle LMNP has an area of 700 square units. The point L is (15, 15) and the point P is (−20, 15). Find one possible pair of answers for M and N

Solution :

Distance between L and P = √[(-20-15)² + (15-15)²]

= √[(-35)² + 0

= 35

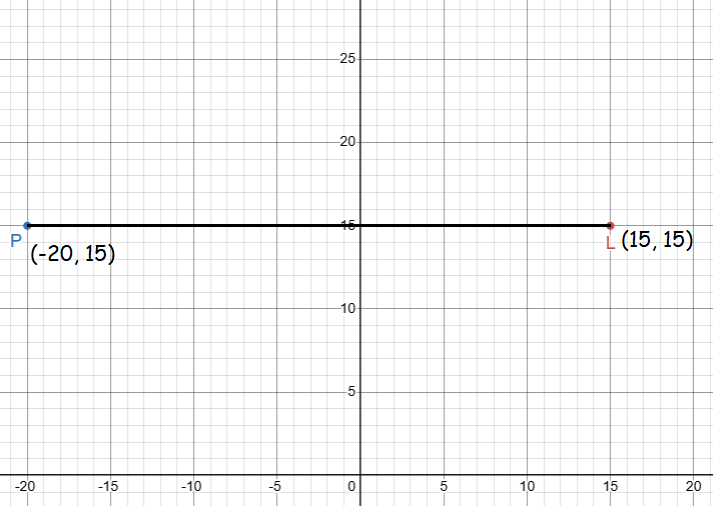
So, length of the rectangle is 35 units

Area of rectangle = 700 square units

length x width = 700

35 x width = 700

width = 700/35

width = 20 units

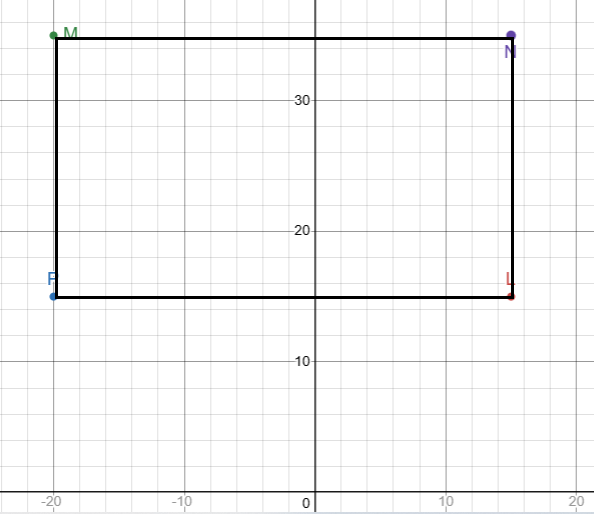
From y-coordinate of P, we have to move horizontally 20 units. So, we get the point 15 + 20 ==> 35 at this position. 

M(-20, 35) and from -20, we have to move 35 units. 

N(15, 35) is the required co-ordinate.

Example 3 :

Square LMNO is shown in the diagram below.

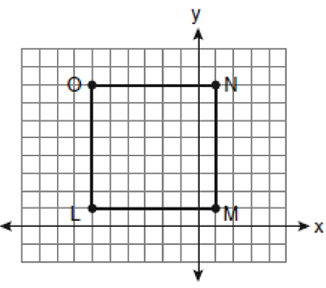
What are the coordinates of the midpoint of diagonal LN?

Solution :

The coordinates of L (-6, 1) O(-6, 8) N(1, 6) and M(1, 1)

Midpoint of the diagonal LN = (x₁ + x₂)/2, (y₁ + y₂)/2

= (-6 + 1)/2, (1 + 6)/2

= (-5/2, 7/2)

Example 4 :

A(−2, 2), B(6, 5), C(4, 0), D(−4, −3)

Prove: ABCD is a parallelogram but not a rectangle

Solution :

Angle measure at each vertex is 90 degree. By proving the lines which are perpendicular, then we can prove that it is a rectangle.

Slope of AB = (y₂ - y₁)/(x₂ - x₁)

= (5 - 2) / (6 - (-2))

= 3/(6 + 2)

= 3/8

Slope of BC = (y₂ - y₁)/(x₂ - x₁)

= (0 - 5) / (4 - 6)

= -5/2

If two lines are perpendicular, then the product of their slopes will be equal to -1.

The product of slopes of AB and BC is not equal -1, then they will not create 90 degree. So, it must be a rhombus.

Example 5 :

Quadrilateral ABCD has vertices A(−5, 6), B(6, 6), C(8, −3), and D(−3, −3).

Prove: Quadrilateral ABCD is a parallelogram but is neither a rhombus nor a rectangle. 

Solution :

• In parallelogram, the midpoints of the diagonal will be equal.
• In rhombus, the diagonals will intersect at 90 degree.
• In rectangle, the sides will intersect at 90 degree.

Midpoint of the diagonal AC = (x₁ + x₂)/2, (y₁ + y₂)/2

= (-5 + 8)/2, (6 - 3)/2

= (3/2, 3/2)

Midpoint of the diagonal BD = (x₁ + x₂)/2, (y₁ + y₂)/2

= (6 - 3)/2, (6 - 3)/2

= (3/2, 3/2)

Since the midpoint of the diagonals are the same it must be a parallelogram.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.