HOW TO CHECK IF A RELATION IS A FUNCTION

Let us consider the relation 'f' such that

f : A ---> B

where A and B are not empty sets. 

If the above relation 'f' is a function, then it has to satisfy the following two conditions. 

(i) Domain 'f' must be equal to A. That is, every element of A must have an image in B. 

(ii) Every element of A must have only one image in B. 

Example : 

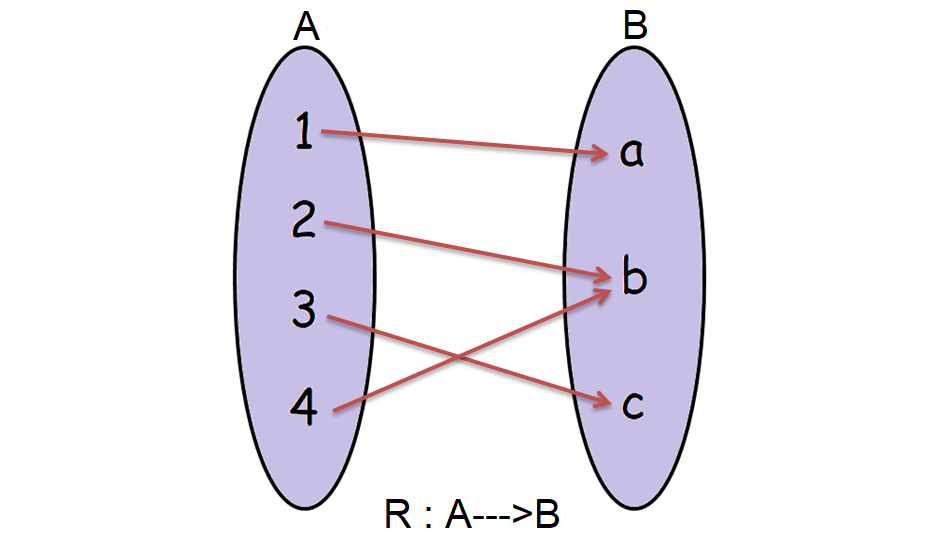
Let A  =  {1, 2, 3, 4} and B  =  {a, b, c}. 

Consider the relation R given below which maps the elements from A to B. 

R  =  {(1, a), (2, b), (3, c), (4, b)}

In the above relation R, 

Domain (R)  =  A

And also, every element of A has only one image in B. 

So, the relation R is a function. 

It has been illustrated in the picture shown below. 

Vertical Line Test

Vertical line test can be used to check whether the given graph represents a function. 

The following are the steps of vertical line test : 

Step 1 : 

Draw a vertical line at any where on the given graph. 

Step 2 : 

We have to check whether the vertical line drawn on the graph intersects the graph in at most one point.

Step 3 : 

If the vertical line intersects the graph in at most one point, then the given graph represents a function. 

If the vertical line intersects the graph in more than one point, then the given graph does not represent a function. 

Caution : 

For some graphs, the vertical line will intersect the graph in one point at one position and more than one point at a different position.

In the above situation, the graph will not represent a function. 

Key Concept :

A graph represents a function only if every vertical line intersects the graph in at most one point.

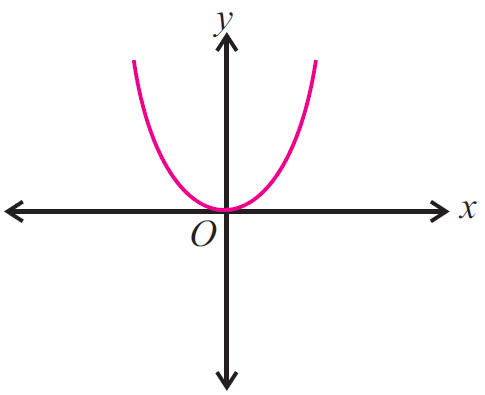
Example : 

Use the vertical line test to determine whether the following graph represents a function.

Step 1 : 

Draw a vertical line at any where on the given graph. 

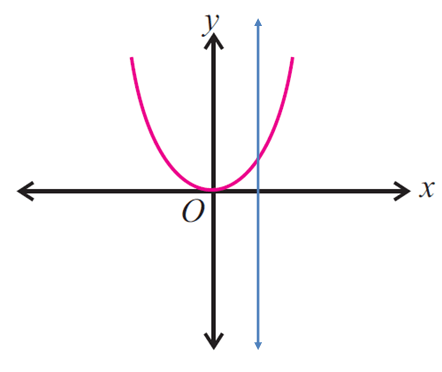
Step 2 : 

We have to check whether the vertical line drawn on the graph intersects the graph in at most one point.

Step 3 : 

In the above graph, the vertical line intersects the graph in at most one point, then the given graph represents a function. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.