HOW TO CALCULATE LENGTH OF CHORD IN CIRCLE

Example 1 :

A chord is 8 cm away from the center of a circle of radius 17 cm. Find the length of the chord.

Solution :

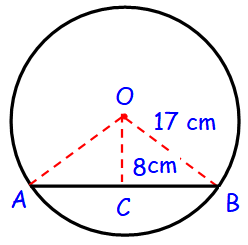
Here the line OC is perpendicular to AB, which divides the chord of equal lengths.

In Δ OCB,

OB²  =  OC² + BC²

17²  =  8² + BC²

BC²  =  17² - 8²

BC  =  √(17² - 8²)

BC  =  √289 - 64

BC  =  √225

BC  =  √(15 ⋅ 15)

BC  =  15 cm

Length of chord  =  AB  =  2 (Length of BC)

  =  2 (15)

=  30 cm

Hence the length of chord is 30 cm.

Example 2 :

Find the length of a chord which is at a distance of 15 cm from the center of a circle of radius 25 cm.

Solution :

Distance of chord from center of the circle  =  15 cm

Radius of the circle  =  25 cm

Length of chord  =  AB

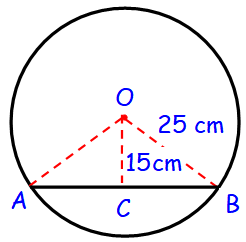
Here the line OC is perpendicular to AB, which divides the chord of equal lengths.

In Δ OCB,

OB²  =  OC² + BC²

25²  =  15² + BC²

BC²  =  25² - 15²

BC  =  √(25² - 15²)

BC  =  √625 - 225

BC  =  √400

BC  =  √(20 ⋅ 20)

BC  =  20 cm

Length of chord  =  AB  =  2 (Length of BC)

  =  2 (20)

=  40 cm

Hence the length of chord is 40 cm.

Example 3 :

A chord of length 20 cm is drawn at a distance of 24 cm from the center of a circle. Find the radius of the circle.

Solution :

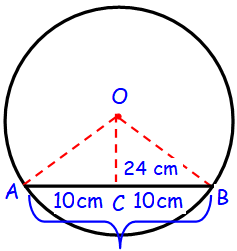
Here the line OC is perpendicular to AB, which divides the chord of equal lengths.

In Δ OCB,

OB²  =  OC² + BC²

OB²  =  24² + 10²

BC²  =  576 + 100

BC²  =  676

BC  =  √676

BC  =  √(26 ⋅ 26)

BC  =  26  cm

Hence the radius of the circle is 26 cm.

Example 4 :

A line which is perpendicular to the radius of the circle through the point of contact is called a ___

(a) tangent    (b) chord    (c) normal     (d) segment

Solution :

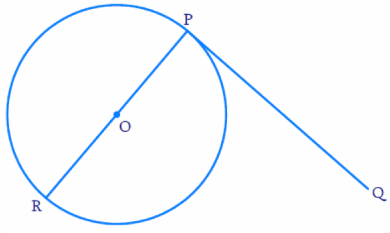
Here the line OP is perpendicular ot PQ. So, the answer is tangent.

Solve for x. Assume that lines which appear tangent are tangent.

Example 5 :

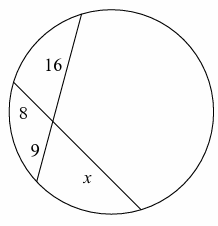
Solution :

When chords are intersecting inside the circle,

8⋅x = 9⋅16

x = (9 ⋅16)/8

x = 9⋅2

x = 18

So, the value of x is 18.

Example 6 :

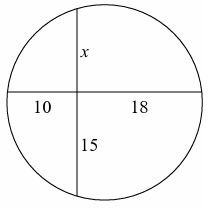
Solution :

When chords are intersecting inside the circle,

10 ⋅ 18 = x ⋅ 15

x = (10 ⋅ 18)/15

x = 180/15

x = 12

So, the value of x is 12

Find the segment length indicated. Assume that lines which appear to be tangent are tangent.

Example 7 :

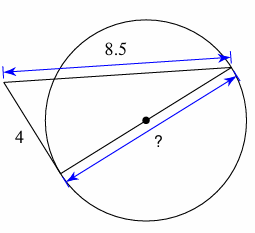
Solution :

The line which touches the circle is the tangent and it make the right angle with the diameter of the circle.

Let x be the diameter of the circle.

Using Pythagorean theorem,

8.5² = 4² + x² 

72.25 = 16 + x² 

x² = 72.25 - 16

x² = 56.25

x = √56.25

x = 7.5

So, the diameter of the circle is 7.5 cm.

Example 8 :

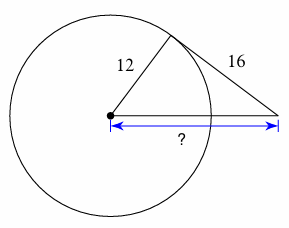
Solution :

The line which touches the circle is the tangent and it make the right angle with the diameter of the circle.

Let x be the length of the chord of circle.

Using Pythagorean theorem,

x² = 12² + 16²

= 144 + 256

= 400

x = √400

x = 20

Example 9 :

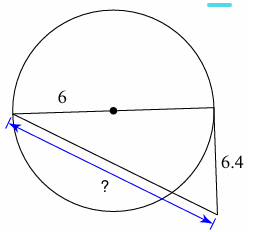
Solution :

Radius = 6 units

Diameter = 12

Let x be the missing side.

x² = 12² + (6.4)²

x² = 144 + 40.96

x² = 184.96

x = √184.96

= 13.6

So, the measure of the missing side is 13.6 units.

Example 10 :

PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P & Q intersect at a point T. Find the length of TP.

Solution :

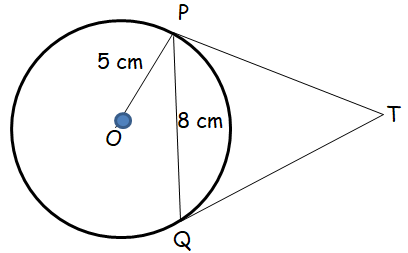
We draw a line from center to T. 

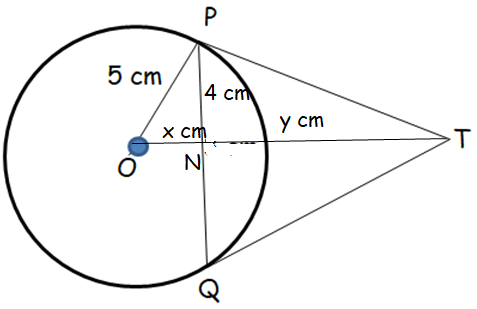
In the triangle PON,

OP² = ON² + PN²

5² = x² + 4²

25 - 16 = x²

x² = 9

x = 3 cm

Then ON is 3 cm.

In triangle POT,

OT² = OP² + PT²

(3 + y)² = 5² + PT²

PT² = (3 + y)² - 25 ----(1)

In triangle PNT,

PT² = PN² + NT²

PT² = 4² + y² ----(2)

(3 + y)² - 25 = 4² + y²

9 + 6y + y²- 25 = 16 + y²

6y - 16 = 16

6y = 16 + 16

6y = 32

y = 32/6

y = 5.33 cm

Applying the value of y in (2), we get

PT² = 4² + 5.3²

= 16 + 28.09

= 44.09

PT = √44.09

PT = 6.64

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.