HORIZONTAL AND VERTICAL TRANSLATIONS

Translation :

One type of transformation is a translation.

A translation can move the graph of a function up, down, left or right.

Note :

The translation occurs when the location of a graph changes but not its shape or orientation.

In other words, a translated graph is congruent to the original graph.

Vertical and horizontal translations are types of transformations with equations of the forms

y - k = f(x)

y = f(x) + k

Mapping :

Points on the original graph correspond to points on the transformed, or image, graph. The relationship between these sets of points can be called a mapping.

Example 1 :

Sketch the graph of y = |x - 4| + 3.

Solution :

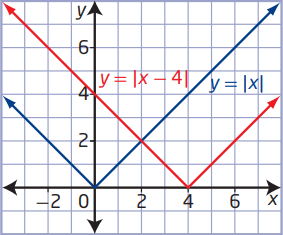
To find the graph of y = |x-4|, we start with the graph of y = |x| (base graph).

By comparing y = x| and y = |x-4|, we see horizontal translation.

Key point :

Here h = 4 > 0, so we move the base graph 4 units towards right side.

Now to sketch the graph of y = |x - 4| + 3, we take

y = |x-4| as base graph.

Here k is 3 > 0, so we move the graph y = |x-4| 3 units up.

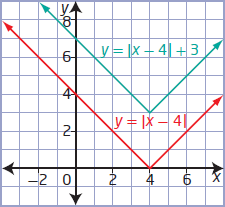
In general, the transformation can be described as

(x, y) → (x + 4, y + 3)

Example 2 :

Describe the translation that has been applied to the graph of f(x) to obtain the graph of g(x). Determine the equation of the translated function in the form

y - k = f (x - h)

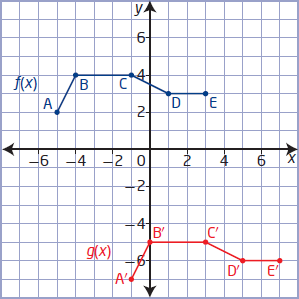
Solution :

By observing x-coordinates of f(x) and g(x),

h = 4 > 0. So, move the base graph 4 units right side.

k = -9 < 0. So, move the base graph 9 units downward.

y - k = f (x - h)

Applying the values of h and k, we get

y + 9 = f(x - 4)

Example 3 :

What vertical translation is applied to y = x² if the transformed graph passes through the point (4, 19)?

Solution :

When we apply x = 4 in the base graph y = x², we get  y as 16.

By analyzing the y-coordinate of the given point, we have 19.

16 + 3 = 19

So, the required vertical translation is 3 units up.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.