HIGHEST COMMON FACTOR

Let us consider the numbers 36 and 48.

We can use divisibility rules to find the factors of 36 and 48.

Factors of 36 : 

1, 2, 3, 4, 6, 9, 12, 18 and 36

Factors of 48 :

1, 2, 3, 4, 6, 8, 12, 16, 24 and 48

Common factors of 36 and 48 :

1, 2, 3, 4, 6 and 12

As factors of a number are finite, we can think of the Highest Common Factor of numbers, shortly denoted as HCF.

Think about the following situation.  

Consider the rods of length 8 feet and 12 feet. We have to cut these rods into pieces of equal length. How many pieces can we get ? What will be the length of the longest piece that is common for both the rods ?

The rod of 8 feet can be divided into small rods of length 1 foot or 2 feet or 4 feet (These are factors of 8). The rod of 12 feet can be divided into small rods of length 1 foot or 2 feet or 3 feet or 4 feet or 6 feet (These are factors of 12).

This is represented as follows :

First, it is possible to cut the 8 feet and 12 feet rods equally into 1 foot rods.

Number of pieces = (8, 12). 

Second, it is also possible to cut the 8 feet and 12 feet rods equally into 2 feet rods.

Number of pieces = (4, 6). 

Third, it is also possible to cut the 8 feet and 12 feet rods equally into 4 feet rods.

Number of pieces = (2, 3). 

The length of the pieces that are common to both the rods (as given above) are of length 1 foot, 2 feet and 4 feet (i.e., common factors of 8 and 12).

Hence, the HCF of 8 and 12 is the length of the longest rod i.e., 4 feet that can be cut equally from the rods of length 8 feet and 12 feet.

So, the Highest Common Factor (HCF) of two numbers is the greatest factor that is common to both of them. The Greatest Common Factor of the numbers x and y can be written as GCF (x,y).

Note : 

● The Highest Common Factor (HCF) is also called as the Highest Common Divisor (HCD) or Greatest Common Factor (GCF)

● HCF (1, x) = 1. 

● HCF (x, y) = x, if y is a multiple of x.

For example, HCF (3, 6) = 3.

● If the HCF of two numbers is 1, then the numbers are said to be co-primes or relatively prime.

Here, the two numbers can both be primes as (5, 7) or both can be composites as (14, 27) or one can be a prime and other a composite as (11, 12).

Finding GCF by Division Method

Example 1 : 

Find the HCF of the numbers 16 and 24. 

Solution :

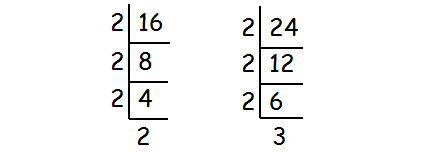
The product of common factors of 16 and 24 is

=  2 x 2 x 2

=  8

So, HCF (16, 24)  =  8

Finding GCF by Factor Tree Method

Example 2 : 

Find the GCF of the numbers 18, 24 and 30. 

Solution :

Find the factors of 18, 24 and 30 by factor tree method. 

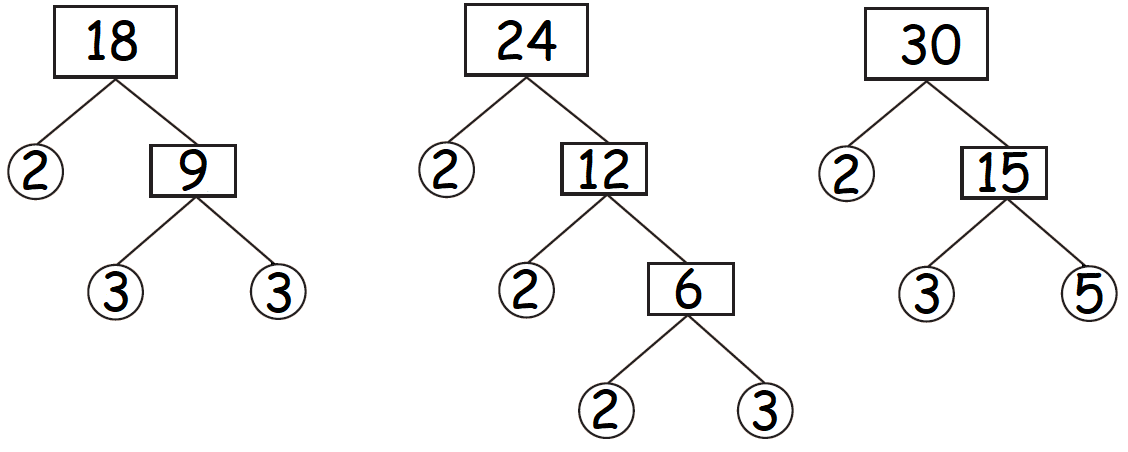
Let us find the factors of 18, 24 and 30 (use of  divisibility test rules will also help).

Factors of 18 :

1, 2, 3, 6, 9, 18

Factors of 24 :

1, 2, 3, 4, 6, 8, 12, 24

Factors of 30 :

1, 2, 3, 5, 6, 10, 15, 30

The factors that are common to all the three given numbers are 1, 2, 3 and 6 of which 6 is the highest.

Therefore HCF (18, 24, 30) = 6.

Note :

1 is a trivial factor of all numbers.

Finding GCF by Prime Factorization Method

Example 3 : 

Find the GCF of the numbers 60 and 96. 

Solution :

Write the prime factors of 60 and 76. 

60  =  2 x 2 x 3 x 5 

96  =  2 x 2 x 2 x 2 x 2 x 3

The prime factors that are common to 60 and 96 are

2, 2 and 3

Product of common prime factors :

=  2 x 2 x 3

=  12

Hence, HCF (60, 96) = 12.

Example 4 : 

Martin says that 6 is a common factor of 42, 36 and 50. Is he correct?

Solution :

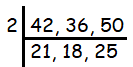
From here, we know that 42, 36 and 50 are divisible by 2. In the second step, we have 21, 18 and 25. Here 21 and 18 are divisible by 3 but 25 is not. So, we cannot decide 3 is the factor. Then 6 is not a factor of 42, 36 and 50.

Example 5 :

Alannah has two lengths of ribbon. One length of ribbon is 36 cm long and the other length is 45 cm long. Alannah wants to cut lengths of ribbon into shorter lengths that are of equal length. Alannah does not want any ribbon left over. What is the longest possible length for each of the shorter lengths of ribbon?

Solution :

To find the length of the ribbon which is common for both, we have to find the common factor for both 36 and 45.

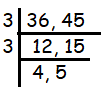
highest common factor = 3 x 3

= 9 

So, the largest possible length of the ribbon is 9 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.