HIGH SCHOOL MATH PRACTICE TEST

Problem 1 :

{Prime numbers which have 4 as a factor} is a

 (A) Empty set     (B) Set of all prime numbers    

 (C) Singleton set

Solution :

Prime numbers is a number which is divisible by 1 and itself.

Problem 2 :

Joy has  thin rods, one each of every integer length from  1 cm through 30 cm. She places the rods with lengths  3 cm, 15 cm, and  7 cm on a table. She then wants to choose a fourth rod that she can put with these three to form a quadrilateral with positive area. How many of the remaining rods can she choose as the fourth rod?

 (A) 40               (B) 10             (C) 20

Solution :

Polygon inequality theorem :

The longest side must  be shorter than the sum of the rest.

Let x be the unknown side.

If x is the longest side, then

3+15+7 > x 

25 > x

If 15 is the longest side, then 

3+x+7 > 15

x + 10 > 15

x > 5

So the range is 5 < x < 25.

between 5 to 25, we have 19 numbers. But we have two values included in the list. Those are 7 and 15. 

19 - 2  =  17

So the length of fourth rod is 17 cm.

Problem 3 :

In a class of 35 students, 28 students passed in History, 22 in Mathematics and 18 in both Subjects.

Find the number of students who passed in (i) History alone and (ii) Mathematics alone

Solution :

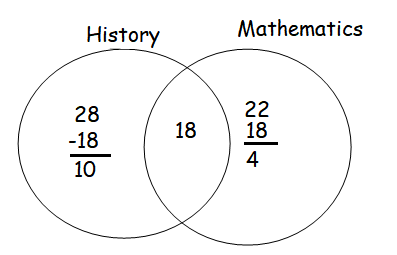
Number of students who passes history alone  =  10

Number of students who passed in math alone  =  4

Problem 4 :

Subtract 2x³–3x² – 1 from x³ + 5x²–4x–6

 (A) –x³-8x²+4x+5      (B) –x³-8x²-4x-5   

(C) –x³+8x²-4x-5

Solution :

  =  x³+5x²–4x–6 - (2x³ – 3x² – 1)

  =  x³-2x³+5x²+3x²-4x-6+1

  =  -x³+8x²-4x-5

Problem 5 :

Find the product of 2x + 3y and x²– x y + y² ?

(A) x³-x²y-xy²+3y³        (B) 2x³-x²y+xy²-3y³ 

(C) 2x³+x²y-xy²+3y³

Solution :

(2x+3y)(x²– xy + y²)

  =  2x³-2x²y+2xy²+3x²y-3xy²+3y³

  =  2x³+x²y-xy²+3y³

Problem 6 :

Expand (11a-7b)²

 (A) 121a²+154ab-49b² (B) 121a²-154ab+49b² 

(C) 121a²+154ab-49b²

Solution :

a  =  11a and b  =  7b

(a-b)²  =  a²-2ab+b²

(11a-7b)²  =  (11a)²-2(11a)(7b)+(7b)²

=  121a²-154ab+49b²

Problem 7 :

If the values of a + b and a – b are 7 and 4 respectively, find the values of a² + b² and ab.

 (A) 15/2, 3/4    (B) 35/2, 13/4    (C) 65/2, 33/4

Solution :

a+b  =  7  -----(1)

a-b  =  4  -----(1)

(1)+(2)

2a  =  11

a  =  11/2

By applying the value of a in (1), we get

11/2 + b  =  7

b  =  7-(11/2)

b  =  3/2

a²  =  121/4, b²  =  9/4

a² + b²  =  130/4  ==>  65/2

ab  =  (11/2)(3/2)

ab  =  33/4

Problem 8 :

The factors of x²–2xy-x+2y.

 (A) (x+y)(x-2)      (B) (x-2y)(x-y)    (C) (x-2y)(x-1)

Solution :

x²–2xy-x+2y

  =  x(x-2y)-1(x-2y)

  =  (x-1)(x-2y)

Problem 9 :

What is the remainder when 2x³+3x²+5x+2 is divided by x+1

 (A) -2                 (B) 2             (C) 0

Solution :

Let p(x)  =  2x³+3x²+5x+2 

x+1  =  0

x  =  -1

p(-1)  =  2(-1)³+3(-1)²+5(-1)+2 

  =  -2+3-5+2

  =  -2

So, the remainder is -2.

Problem 10 :

For every real number x, does x² - 1 > 0?

 (A) True         (B) False         (C) Not to decide

Solution :

 x² - 1² > 0

(x-1)(x+1) > 0

Since x is real value, we can take all positive and negative values of x.

It may not be always true. So, the answer is false.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.